| - PR - |
| ＜No3：法規：解答＞ 測量計算の基礎について問う問題である。問題文を図に描いて考えると次のようになる。 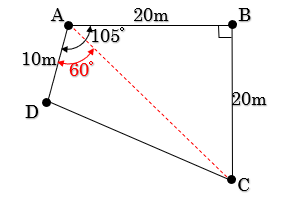 ここで、点AC間に補助線を引くと、三角形ABCは直角二等辺三角形となり∠A＝∠C＝45°となる。よって、ACの長さは次のようになる。  次に三角形ACDの高さは、AD×sin（105°－45°）となるため、ACの長さを考えると、三角形ACDの面積A1は次のように計算される。  直角二等辺三角形ABCの面積A2は、  であるため、四角形ABCDの面積Aは次のようになる。 よって、ア：28.284ｍ、イ：322.474㎡となり、最も近い値は2.となる。 ＜ 別 解 ＞ 図のように点A，Dに対して補助線を引くと次のように計算できる。 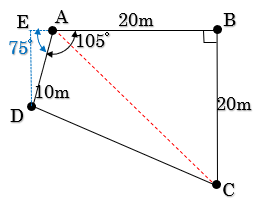 ここで、EA及びEDの長さを求めると次のようになる。  よって、台形BCDEの面積A2は次のようになる。  ここから、三角形ADEの面積を引けば、四角形ABCDの面積を求めることができる。 三角形ADEの面積A1は、A1=2.588×9.659×0.5≒12.499㎡ であるため、 四角形ABCDの面積Aは次のようになる。 A=334.969-12.499=322.470㎡ よって、ア：28.284ｍ、イ：322.470㎡ となり、最も近い値は2.となる。 |
| 解答： ２ |