| - PR - |
| <No26:応用(路線):解答> 単曲線の計算に関する問題である。問題文のように弦長を求めるには、次のような手順で解答すればよい。 ①次図のように補助線O-Dを描き∠(A-O-D)を求める。 単曲線の特徴の1つとして、次のように交角(I)= ∠(A-O-B)また、∠(A-O-C) =I/2となる。 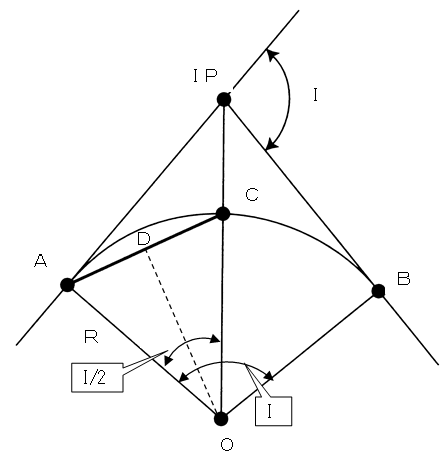 ∠(A-O-D)=∠(D-O-C) = I/4 であるため、∠(A-O-D)は 112°÷ 4 = 28° となる。 ② 弦長を求める。 弦長(A-C)は、直線(A-D)×2であるため、三角形(A-O-D)に注目して、三角関数により、直線(A-D)を求めると、 R×sin(I/4) = 200m×sin28°= 200×0.46947= 93.894m となる。 ※三角関数表により、sin28°=0.46947 とする。 よって、弦長(A-C)は、 93.894m × 2 = 187.788mとなり、最も近い値は、3の188mとなる。 |
| 解答: 3 |