<No27:応用(用地):解答>
座標法による面積計算に関する問題であるが、座標点が移動した場合の面積差を求める問題。
次の手順で解けばよい。
① 問題文の整理
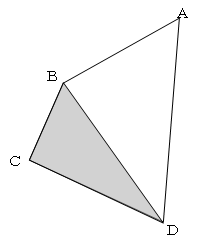
問題では図のような土地でC点の座標値を誤った場合に面積に与える影響を求めるため、
BCDの面積のみを考えればよい。
② 正しい座標値の面積
| 点 |
X(m) |
Y(m) |
Yn+1―Yn―1 |
X ×(Yn+1―Yn―1) |
| B |
+35.5 |
+30.2 |
26.5-38.2=-11.7 |
-11.7×35.5=-415.35 |
| C |
+26.4 |
+26.5 |
38.2-30.2=+8.0 |
8.0×26.4=+211.20 |
| D |
+17.9 |
+38.2 |
30.2-26.5=+3.7 |
3.7×17.9=+ 66.23 |
| 合計(倍面積) |
-137.92 |
| 面積(絶対値) |
68.96 |
③ 誤った座標値の面積
| 点 |
X(m) |
Y(m) |
Yn+1―Yn―1 |
X ×(Yn+1―Yn―1) |
| B |
+35.5 |
+30.2 |
26.4-38.2=-11.8 |
-11.8×35.5=-418.90 |
| C |
+26.5 |
+26.4 |
38.2-30.2=+8.0 |
8.0×26.5=+212.00 |
| D |
+17.9 |
+38.2 |
30.2-26.4=+3.8 |
3.8×17.9=+ 68.02 |
| 合計(倍面積) |
-138.88 |
| 面積(絶対値) |
69.44 |
④ 面積の較差
69.44㎡ - 68.96㎡ = 0.48㎡
|
| 解答: 2 |
|
