| - PR - |
| <No26:応用(路線):解答> 単曲線設置と方向角の計算を組み合わせた問題である。次のように解答すればよい。 ① 問題文に与えられた数値を図に描く 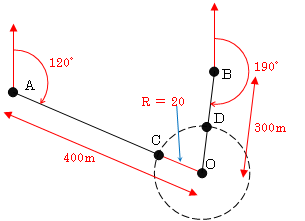 ② AC、BDの長さを求める ①の図より、AC=400-20=380m 、 BD=300-20=280m となる。 ③ 交角(I)を求める 図のように円の中心をOとした場合のBCをC点、ECをD点と考えれば、交角Iは単曲線の性質から∠AOB(∠COD)と同じになる。 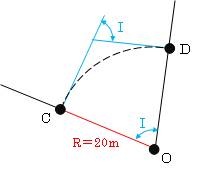 次に∠AOBの大きさを求めると次のようになる。 次図のようにまず点Oから点Aの方位角を考えると、120°+180°=300° 点Oから点Bへの方位角は190°+180°-360°=10° よって、∠AOB=(360°-300°)+10°=70°となる。 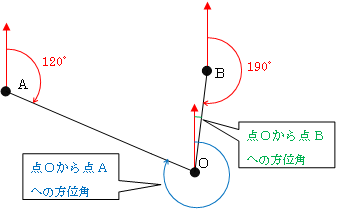 ④ 曲線長CDを求める 単曲線の曲線長(CL)は、CL=RI°×π/180°により求められる。 よって、曲線長CDの長さは、20m×70°×(π/180°)=24.438m よって、AC~CD~BDの路線長は、 380m+280m+24.438m=684.438mとなる。 |
| 解答: 3 |