| ��11��
��i�P�j���၄
|
|
�w���W
|
�x���W
|
|
�f�_�̍��W�l
|
110.96
|
123.81
|
|
�d�_�̍��W�l
|
120.62
|
142.09
|
|
�e�_�̍��W�l
|
110.96
|
138.95
|
��蕶�͂s2���s1�Ȃ̂łs1���s2��274���ƂȂ邱�Ƃɒ��ӁB
���̕\�ł͕��ӂ̂܂܂̕\�L�ɂ��Ă��邪T1����݂������p�Ɉ��������Čv�Z����B
|
��B�_
|
�����_
|
���p
|
�����p
|
����
|
��X
|
��Y
|
|
�w
|
�x
|
|
T2
|
T1
|
|
94��
|
|
|
|
T1
|
106.41
|
125.74
|
|
T1
|
G
|
63��
|
337��
|
4.94
|
+4.55
|
-1.93
|
G
|
110.96
|
123.81
|
|
T1
|
E
|
135��
|
49��
|
21.66
|
+14.21
|
+16.35
|
E
|
120.62
|
142.09
|
|
T1
|
F
|
157��
|
71��
|
13.97
|
+4.55
|
+13.21
|
F
|
110.96
|
138.95
|
��11��@��i�Q�j���၄
|
�w���W
|
�x���W
|
|
110.96
|
130.70
|
�o�_�̍��W�l
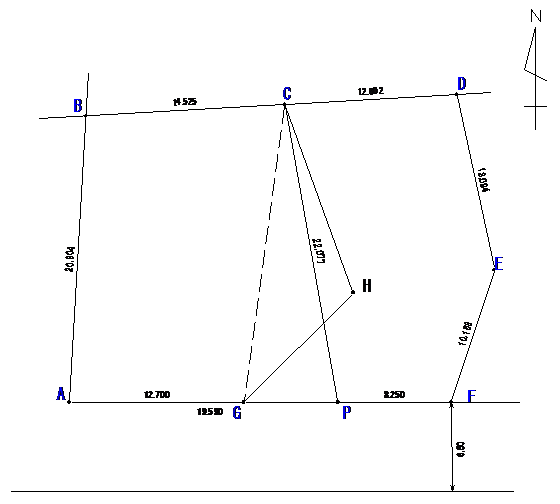
��CHG115��(�����̋��p)�A��CH��14.62m�A��HG��11.30m�̓�Ӌ��p��
�O�p�`CHG�̖ʐς����߂��74.863�u
S��1/2bcsinA��1/2(14.62�~11.30)�~sin115����74.86374�E�E�E
Gx��Ax��Fx��Px��110.96�@�̂ɐ�����Cx�|Gx��21.730�Ȃ̂ŁA
��ӂɂ������GP�̒�����6.890���ƂȂ�i74.863��21.730�~2��6.890�j�B
Py��Gy�{6.89��123.81�{6.89��130.70
�����ł�H�_�̍��W�����߂�K�v�͂Ȃ��B���ϕό`�ɂ����H�_��P�_�ɂ����������邽�߂ł���B
��11��
��i�R�j���၄
|
|
Xi
|
Yi
|
Yn+1�|Yn-1
|
Xi (Yn+1�|Yn-1)
|
|
�b
|
132.69
|
126.80
|
�{ 8.68
|
�{1151.7492
|
|
�c
|
133.43
|
139.38
|
�{15.29
|
�{2040.1447
|
|
�d
|
120.62
|
142.09
|
�| 0.43
|
�| 51.8666
|
|
�e
|
110.96
|
138.95
|
�|11.39
|
�|1263.8344
|
|
�o
|
110.96
|
130.70
|
�|12.15
|
�|1348.1640
|
|
|
|
�Q�r
|
|
�{ 528.0289
|
|
|
|
�b�r�b
|
264.01445
|
��11��@��i�S�j���၄
|
