| - PR - |
|
�� 11��
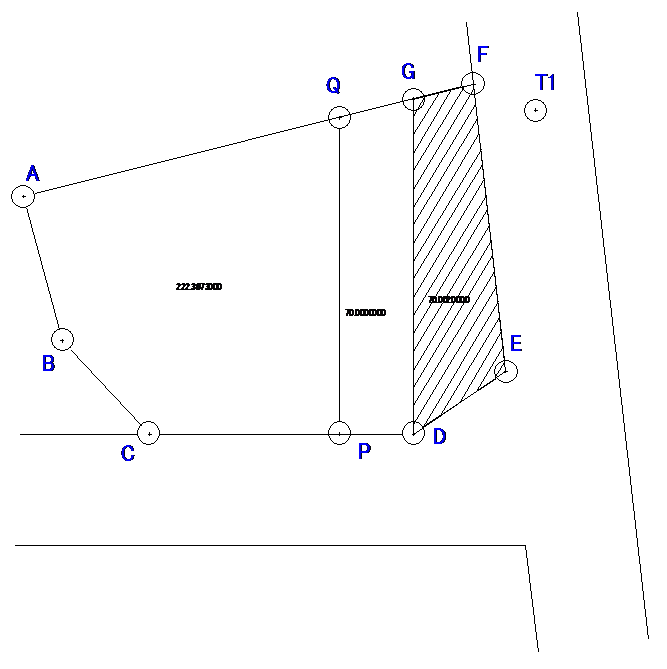
��L�̑��ʃf�[�^�́A��L����}�Ɏ����Z�p�`�`�a�b�c�d�e�̓y�n�n�̊ϑ��̌��ʂł���B���̌��ʂɊ�Â��A�ʎ���11�ⓚ�ėp����p���āA����1����5�܂ł̖�ɓ����Ȃ����B �Ȃ��A���W�l �A�����y�ѕӒ��́A�v�Z���ʂ̏����_�ȉ���O�ʂ��l�̌ܓ����A�����_�ȉ����ʂ܂łƂ��A�ʐςɂ��ẮA�v�Z���ʂ̏����_�ȉ���O�ʂ��̂Ă��A�����_�ȉ����ʂ܂łƂ��邱�ƁB�܂��A�����p�́A�x��P�ʂƂ��āA�����_�ȉ����ʂ��l�̌ܓ����邱�ƁB ��(2)�ɂ��ẮA���ėp���̊Y�����Ɍv�Z�ߒ��𖾂炩�ɂ��邱�ƁB
�k���ʌ��ʁl �s1�́A��B�_�ł���B �k�͂w���������Ɉ�v����B
 |
||||||||||||||||||||||||||||
|
��11��i�P�j���၄
�e�_�̍��W�l
|
|
��11��i�Q�j���၄
��i�Q�j�̌v�Z�ߒ�
�w�v�Z�ߒ������x�ł����āw�v�Z�����������x�ł͂Ȃ����Ƃɒ��ӁB �ʐς����`�̍����Ə����ꔭ�ŋ��߂�����͑��݂��Ȃ��̂ŁA���Z���s���ĉ邾���� �[���ł���B�Ȃ����N�x�͔��v�Z�ɂ����W�v�Z���̂��̂͏ȗ����Ă���B |
|
��11��i�R�j���၄
|
|
��11��i�S�j���၄
|