第６問

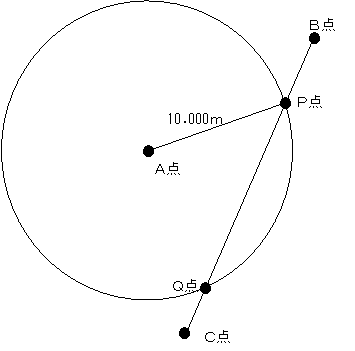
次の図のように、Ａ点を中心とする半径10.00ｍの円、Ｂ点とＣ点とを結ぶ直線ＢＣとの交点がＰ点とＱ点である場合に、Ｐ点及びＱ点の座標値として最も近いものの組合せとして正しいものは、後記１から５までのうちどれか。ただし、Ａ点の座標は、Ｘ＝−2310.00  Ｙ＝1660.00、  Ｂ点の座標は、Ｘ＝−2295.00   Ｙ＝1675.00、  Ｃ点の座標は、  Ｘ＝−2325.00  Ｙ＝1660.00である。

直線の方程式　y＝ax＋b（1式）　円の方程式　r²＝x²＋y²　(2式)であるから、2式のyに1式を代入・展開し、二次方程式の根の公式によって解く。

0＝x²＋y²−r² ＝(a+1)x²＋2abx＋b²−r²(展開式)

１式のaおよびbを求める前に、円中心からの相対位置関係とするため、座標変換を施し、Ａ(0,0)、Ｂ(+15,+15)、Ｃ(-15,0)としておく。上記方程式は円中心を原点として解く簡易形だからである。

Δｘ＝ 15.00−(−15.00)＝30.00　

Δｙ＝ 15.00−0.00＝15.00

∴　ａ＝15.00/30.00＝0.50

上記座標差から、ｙ＝0のときｘ＝−15.00なので、0＝0.5x＋ｂ＝−7.5＋b　∴b＝＋7.50

検算　ｘ＝15.00 ： ｙ＝0.5×15.00−7.50＝0.00　(Ｃ点のY座標)

ここで(2式)に(1式)を代入して展開した式にa、bを代入すると次のようになる。

Ａ ＝ a²＋1＝＋1.25、B＝2ab＝＋7.5、C＝b²−r²＝−43.75

�I ＝ −B±√（B²−4AC）/2A＝(-7.5±√(56.25+218.75))/2.50

＝ −3.000±6.633　→　＋3.633 ,−9.633

(選択肢の下2桁を確定させるために下3桁まで算出し、さらに相対座標を実座標に変換)

ｘ＝ ＋3.633の場合　　Ｘ＝ +3.633−2310.00 ＝−2306.37

ｙ＝ 0.5×3.633＋7.50＋1660.00 ＝ 1669.32

ｘ＝ −9.633の場合　　Ｘ＝ -9.633−2310.00 ＝−2319.63

ｙ＝ 0.5×（-9.633）＋7.50＋1660.00 ＝ 1662.68

※　H18出題済。解答肢はそれぞれ1cm程度の違いでしかないため、上記のような　厳密な答解を導く必要があるため時間が無ければ捨て問とすべきであろう。