第３問

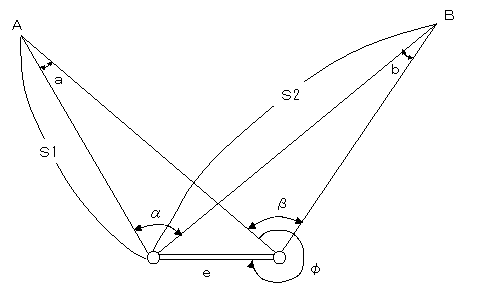
次の観測結果を用いて偏心計算を行い、図中の角αの値に最も近いものは、次の１から５までのうちどれか。

1.    46°22′36″

2.    46°23′16″

3.    46°24′36″

4.    46°25′56″

5.    46°26′36″

偏心補正計算であるが、形態にとらわれず参考書の公式どおりでよい。

下記の公式のSにS1を代入するとａが、S2を代入するとｂが得られる。

ただし、bを求めるときのθはφ−βであり、ａのときはφそのものを使う

δ＝ｅsinθ/S（ラジアン表記のため角度秒に変換する必要がある）

αはβにおいてS1、S2の平行線を引いて図示することができる。

ａ＝0.8m×sin285°30′÷800m＝0.0009636304…

（ａ″＝a×ρ″≒193″＝ 0°3′13″）

ｂ＝0. 8m×sin239°5′24″÷1200m＝0.0005719835・・・・

（ｂ″＝ｂ×ρ″≒ 114″＝0°1′54″）

α＝β−a＋ｂ＝46°23′17″よって最も近い46°23′16″を選択する。

　※ρ″＝ 2×10^５ で計算