| - 平方根の手計算による解法 - |
|
|
手計算によるルートの解法は、以下に挙げる３通りの方法が考えられるが、平方根の解法は、どれか一つの方法を使うと言うよりは、問題の形式（ルート中の数字）に合わせて使い分けることが大切である。また、手計算は「慣れ」であるため、普段から練習する事が大切である。
1. 近似値法
2. 加減法
3. 分解法
上記の方法について、以下に記述する。
|
|
１． 近似値法
√？とは、２乗して？になる数のことを言う。
そこで、√0.0145 を例に挙げて考えると次のようになる。
・ 0.5×0.5＝0.25 ＜ずいぶん大きい…＞
・ 0.2×0.2＝0.04 ＜まだ大きい…＞
・ 0.1×0.1＝0.01 ＜ちょっと小さい…＞
・ 0.13×0.13＝0.0169 ＜ちょっと大きいか…＞
・ 0.12×0.12＝0.0144 ＜こんなものだな･･･＞
よって、√0.0145 ≒ 0.12 とする。
この方法は、いわば「自分で適当に数を合わせていく方法」であり、平方根の計算キーが無いような電卓を使うときにもよく使用される。
|
|
２． 加減法
１.同様に√0.0145を例にとり考える。
※ 手順を以下に、計算結果をその次に記述する。
1. まず、小数点の位置を基準として、「２ケタ」に区切る。
2. 次に√の先頭の数字は、「０」であるため、「２乗して０より小さく、０に最も近い数字を見つけだし、（※同じでもよい）次図の０の上（●の位置）に書く。
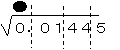
3. √の下に、「０－０×０＝０」を書き、左図に「０＋０＝０」の計算をしておく。さらに、√中の次の２ケタ「０１」も書く。
4. 左図の０□×□が、右図の「０１」より小さく、「１」に最も近い数字「１」を見つけ出し、√中の０１の上に書き、左図でも「０１＋１＝２」を計算しておく。
5. このとき、右図においても「０１－１＝０」の計算を行い、書いておく。
6. さらに次の２ケタ「４４」を⑤で計算した「０」のとなりに書く。
7. 4.と同様に、左図の「２□×□」が右図の「４４」より小さく、「４４」に最も近くなる数字、「２」を見つけ出し、「４４」の√の上に書く。また、左図にも、「２２×２＝２４」を書き、右図においても、「４４－４４（２２×２）＝０」の計算を行い、書いておく。
※ 以下同様（図参照）にして、計算を進め、解答を得る。
|
|
３． 分解法
まず、小数点の平方根に関して、次のような法則を覚えておくと便利である。
・√0.1＝0.316… → √0.2＝0.447
・√0.01＝0.1 → √0.02＝0.1414… （√2／10）
・√0.001＝0.0316 → √0.002＝0.0447…
・√0.0001＝0.01 → √0.0002＝0.014142… （√２／100）
ここで、前出の√0.01455について、考えてみる。
√0.01455は、√0.0001×√145.5に分けられる。つまり、0.01×√145となり、さらに、0.01×12.04となる。これを計算すれば、0.12となり、近似値が計算される。
|
|
Copyright 2002-2006 (C) MATSUBARA Planning Office