<H16-4-A：問題>

標高27.3mの基準点Aに平板を整置し、求点Bに立てた目標板をアリダードで視準して、読定値として－8.0分画を得た。AB間の水平距離を30.0mとすると、求点Bの標高はいくらか。最も近いものを次の中から選べ。

ただし、器械高は1.2m、目標板の高さは3.0mとする。なお、関数の数値が必要な場合は、巻末の関数表を使用すること。

１．21.9m

２．23.1m

３．24.9m

４．27.9m

５．29.7m

<H16-4-A:解答>

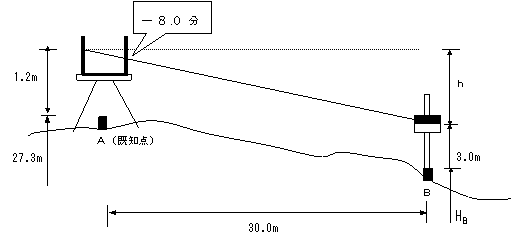
問題文を図に表すと上のようである。また、この図より式を組立てると次のようになる。

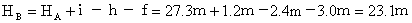
　よって、B点の標高は、23.1mとなる。

解答：２

※H12年度　問題と同じ問題

<H16-4-B：問題>

基準点Aにおいて、上空視界の良い場所に偏心して対空標識を設置し、平板を用いて偏心要素を測定した。その結果は表4-1のとおりであった。偏心点の平面直角座標X、Y及び対空標識の標高Hの値はいくらか。最も近いものを次の中から選べ。

ただし、基準点Aの平面直角座標は、X_A＝＋75,258.82m、Y_A＝－21,640.08m、標高はH_A＝256.66mとし、磁針定数は－8°0′とする。なお、関数の数値が必要な場合は、巻末の関数表を使用すること。

<H16-4-B:解答>

①対空標識の標高計算

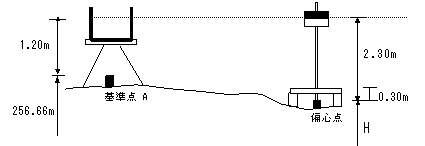
　図より、対空標識の標高は次のようになる。
 H＝ 256.66m＋1.20m－2.30m＋0.30m＝255.86m
※対空標識の標高を求めるため、最後に対空標識までの高さを加える。

 ②偏心点の座標値（X,Y）の計算

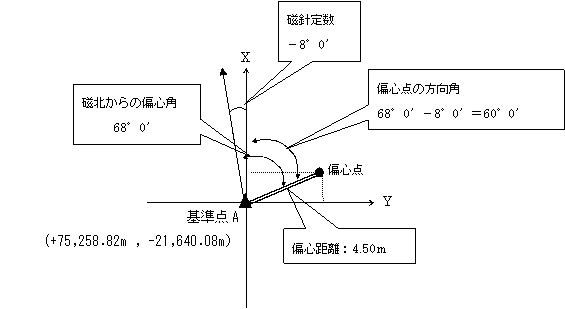
　基準点Aと偏心点の平面的な関係を図に表すと上のようである。ここから、偏心点の座標値を求めると次のようになる。
X＝XA＋ｅ cos60°＝＋75,258.82m＋4.50m×0.500＝＋75,261.07m
Y＝XY＋ｅ sin60°＝－21,640.08m＋4.50m×0.866＝－21,636.18m

解答：４

※H12年度と同じ問題（一部数値変更）

<H16-4-C：問題>

次の文は、標準的な公共測量作業規程に基づいて実施するトータルステーション(以下「TS」という)を用いた細部測量について述べたものである。明らかに問違っているものはどれか。次の中から選べ。

１．TSによる細部測量とは、基準点又はTS点にTSを整置し、地図作成に必要な地形、地物等の測量データを取得する作業をいう。

２．TSによる細部測量は、オンライン方式又はオフライン方式で行う。オフライン方式による細部測量を実施した場合、地形、地物等の数値編集後に、重要事項の確認や補備測量等の現地における作業は全く発生しない。

３．TS点は、基準点に観測機器を整置して放射法により設置し、又はTS点にTSを整置して後方交会法により設置する。

４．TSによる地形、地物等の水平位置及び標高の測定は、放射法、支距法、前方交会法等による。

５．地形は、地性線の位置及び標高値を測定し、図形編集装置によって等高線描画を行う。

<H16-4-C：解答>

１．問題文の通り

２．オフライン方式でもオンライン方式でも、補備測量や重要事項確認などの現地作業は必要。

３．TS点は基準点より放射法が標準。問題文は正しい。

４．地物の位置は、放射法や支距法（オフセット法）が標準。問題文は正しい。

５． 問題文の通り。

解答：２

<H16-4-D：問題>

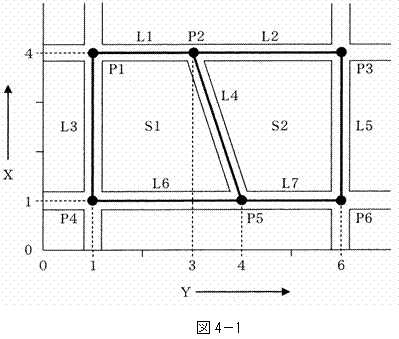
図4-1は、地理情報システム(GIS)のデータを作成するために、ある地域の道路及び道路の中心線を平面上に模式的に表したものである。この図において、P1～P6は道路の交差点を、L1～L7は道路の中心線を、S1、S2は道路の中心線で囲まれた街区面を示している。

また、表4-2は交差点の座標を、表4-3は道路の中心線の始点と終点を示したものである。明らかに間違っているものはどれか。次の中から選べ。

ただし、街区面を構成する道路の中心線の方向は、面の内側からみて時計回りの方向を＋、その反対を－とする。

１．交差点P1のX座標アは、4である。

２．道路の中心線L4の始点イは、P2である。

３．街区面S1は、L3、L1、L4、L6の4本の道路の中心線で構成されている。

４．街区面S2を構成する道路の中心線の方向は、すべて＋である。

５．交差点P1～P6のうち、道路の中心線が奇数本接続する交差点の数は偶数である。

<H16-4-D：解答>

問題各文について考えると次のようになる。

１．Ｘ座標軸より、問題文の通り。

２．L4は街区面Ｓ1から見ると、始点はＰ2である。問題文の通り。

３．問題文の通り。

４．街区面から見た、道路中心線は時計回りを＋としているため、Ｌ5、Ｌ7が－となる。問題文は間違い。

５．Ｐ2とＰ5の交差点が道路が奇数本接続されている。よって交差点数は偶数となる。問題文は正しい。

解答：４