| H16年度 測量士補試験 No3 水準測量 |
|
|
<H16-3-A:問題>
自動レベルの視準線を点検するために、図3-1のように位置A、Bで観測を行い、表3-1の結果を得た。この結果をもとにレベルの視準線を調整するためには、どうすればよいか。最も適当なものを次の中から選べ。
1.位置Bにおいて標尺Iの読定値が1.425mになるように、レベルの十字線を調整する。
2.位置Bにおいて標尺Iの読定値が1.447mになるように、レベルの十字線を調整する。
3.位置Bにおいて標尺Ⅱの読定値が1.464mになるように、レベルの十字線を調整する。
4.位置Bにおいて標尺Ⅱの読定値が1.474mになるように、レベルの十字線を調整する。
5.位置Bにおいて標尺Ⅱの読定値が1.486mになるように、レベルの十字線を調整する。

|
表3-1
|
|
|
|
レベル位置
|
標尺Iの読定値
|
標尺Ⅱの読定値
|
|
A
|
1.357m
|
1.406m
|
|
B
|
1.436m
|
1.475m
|
|
|
|
<H16-3-A:解答>
観測結果から見ると、次のようになり調整が必要である。
(1.406m―1.357m)-(1.475m-1.436m)=0.010m
単純にAでの高低差0.049mを満足させるBにおける標尺Ⅱの読定値は1.485mとなるので、これに近い解答と目星をつけておく。
ここで、Bにおいて標尺Ⅰまでの距離3mで誤差は無視できるが、標尺Ⅱまではその11倍の33mであることに注意する。
0.010m×33/30=0.011mがBにおける標尺Ⅱへの補正量となる。
1.475m+0.011m=1.486m が十字線を調整して読定すべき値である。
解答:5
|
|
|
|
<H16-3-B:問題>
表3-2は、水準測量の誤差と、それを消去するための観測方法を示したものである。ア~ウに入る語句の組合せとして最も適当なものはどれか。次の中から選べ。
|
表3-2
|
|
誤差の種類
|
消去するための観測方法
|
|
ア
|
出発点に立てた標尺が到着点に立つように、レベルの据え付けを偶数回にして観測する。
|
|
イ
|
レベルを両標尺を結ぶ直線上に、両標尺までの距離が等しくなるように整置する。
|
|
ウ
|
標尺の下部付近の視準を避けて観測する。
|
|
|
ア
|
イ
|
ウ
|
|
1.
|
視準線誤差
|
標尺の零点誤差
|
大気の屈折による誤差
|
|
2.
|
標尺の零点誤差
|
視準線誤差
|
大気の屈折による誤差
|
|
3.
|
標尺の零点誤差
|
大気の屈折による誤差
|
視準線誤差
|
|
4.
|
大気の屈折による誤差
|
視準線誤差
|
標尺の零点誤差
|
|
5.
|
大気の屈折による誤差
|
標尺の零点誤差
|
視準線誤差
|
|
|
|
<H16-3-B:解答>
各誤差とその消去方法の組合せは、以下の通りである。
ア → 標尺の零点誤差
イ → 視準線誤差
ウ → 大気の屈折による誤差
解答:2
|
|
|
|
<H16-3-C:問題>
図3-2に示すように、水準点1を新設するため、水準点A、B、C、Dを既知点として水準測量を行い、表3-3の結果を得た。水準点1の標高の最確値はいくらか。最も近いものを次の中から選べ。
ただし、既知点A、B、C、Dの標高は、それぞれHA=55.250m、HB=58.734m、Hc=51.462m、
HD=45.963mとする。なお、関数の数値が必要な場合は、巻末の関数表を使用すること。

|
表3-3
|
|
|
|
路線
|
距離
|
観測高低差
|
|
1 → A
|
5km
|
十2.885m
|
|
1 → B
|
4km
|
十6.380m
|
|
C → 1
|
2km
|
十0.913m
|
|
D → 1
|
2km
|
十6.407m
|
1.52.360m
2.52.364m
3.52.366m
4.52.368m
5.52.373m
|
|
|
<H16-3-C:解答>
①各区間における、重量(P)を求める。
|
区間
|
距離
|
重量(P)
|
整数
|
|
A→1
|
5km
|
1/5
|
4
|
|
B→1
|
4km
|
1/4
|
5
|
|
C→1
|
2km
|
1/2
|
10
|
|
D→1
|
2km
|
1/2
|
10
|
②観測高低差を用いて、各路線の標高を求める。
|
区間
|
観測高低差
|
計算(各水準点標高+比高)
|
水準点1の標高
|
|
A→1
|
-2.885m
|
55.250-2.885
|
52.365m
|
|
B→1
|
-6.380m
|
58.734-6.380
|
52.354m
|
|
C→1
|
+0.913m
|
51.462+0.913
|
52.375m
|
|
D→1
|
+6.407m
|
45.963-6.407
|
52.370m
|
※区間の観測方向に注意する。
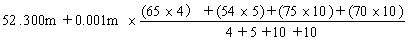 ≒ 52.368m ≒ 52.368m
※ここで、各区間の標高は52.3mまでが共通項であるため、それ以下(小数第2位以降)の数字で計算し、後で加えるものとする。また、小数点は計算上面倒なため、上記のように省略して計算すればよい。
解答 4
|
|
|
|
<H16-3-D:問題>
標準的な公共測量作業規程に基づく1級水準測量を水準点Aから新点Bの間で行い、表3-4の結果を得た。標尺補正後の観測高低差はいくらか。最も近いものを次の中から選べ。
ただし、この観測に使用した標尺定数は20℃において十3μm/m、膨張係数は1.0×10-6/℃とする。
|
表3-4
|
|
|
|
|
区間
|
距離
|
観測高低差
|
温度
|
|
A → B
|
2.Okm
|
-50.8562m
|
25℃
|
1.-50.8603m
2.-50.8566m
3.-50.8561m
4.-50.8558m
5.-50.8521m
|
|
|
<H16-3-D:解答>
標尺補正とは、あらかじめ観測に使用する標尺を基準尺により点検し長さの補正値を求めておき、観測値に対して補正を行うもので、次式により計算される。
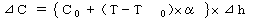
⊿C:標尺補正量 C0:基準温度による標尺定数 T:観測時の測定温度 T0:基準温度 α:膨張係数 ⊿h:高低差(往復観測の平均値)
※膨張係数や標尺定数は各標尺に検定結果(標尺定数表)として備えられている。
ここに、問題文の数値を当てはめると、次のようになる。
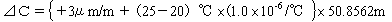 = 0.0004m = 0.0004m
※ μ(マイクロ):1μ=0.000001
標尺補正後の観測高低差 50.8562m+0.0004m = -50.8566m
※標尺補正量は、高低差の絶対値に計算式の符号通りに加える。
解答:2
|
|
|
|
c Matsubara.P.O & c Sey Q’xara |