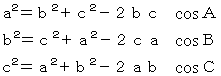| - PR - |
| - PR - |
| - PR - |
|
<H20-2-A�F��>
���@�֘A���i���ʂ̊�j No2�i���p���ʁj�FH19-A�EH20-A No1�i�O�p���ʁj�FH15-D�EH16-C�i�o��@4�^15�j
�@���ʂ̊�i�W���j�Ɋւ�����ł���B
�@�n�����S�ĊC�ʂƂ��čl�����ꍇ�̕��ϓI�ȍ����i���ϊC�ʁj���W�I�C�h�Ə̂��Ă��邪�A���̃W�I�C�h�́A���S�ȑȉ~�̂ł͂Ȃ����ʂ����邽�߁A���ʂ̊�Ƃ��čl����͓̂K���ł͂Ȃ��B�@�@�@ �����ŁA�W�I�C�h�ɋߎ�������]�ȉ~�̂��߂Ēn���̌`���傫�����߂Ă���B����������ȉ~�̂ƌ����B �@���{�ł͂��̏����ȉ~�̂Ƃ��āA���E�e���ŗp�����Ă���f�q�r80�ȉ~�̂𑪗ʖ@�ɂč̗p���Ă���A����𐢊E���n�n�ƌ����B�܂������ɂ��ẮA�����p���ϊC�ʁi�W�I�C�h�j����̍�������Ƃ��Ē�߂Ă���B
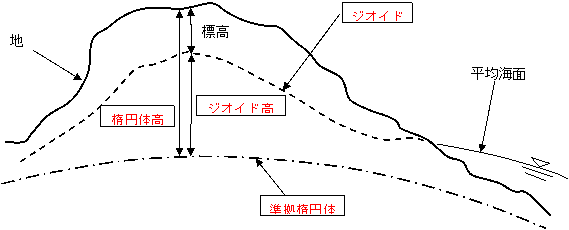
�@��蕶�Ɛ}�ɁA�������Ă͂߂�Ǝ��̂悤�ɂȂ�B
�n���\�ʂ̑啔�����Ă���C�ʂ́A��Ɍ`��ς��Ă���B���̕��ϓI�ȏ�Ԃ𗤒n�����܂ʼn����������z�̖ʂ��i�A�F �W�I�C�h�j �Ƃ�����}�Q�|�P�Ɏ����Ƃ���A�W���́A�i�A�F �W�I�C�h�j�@ ����n�\�܂ł̋����ł���B �@�i�A�F �W�I�C�h�j �́A�n�������̎��ʕ��z�̕s�ώ��Ȃǂɂ���ĉ��ʂ����邽�߁A���ʂł́A �@�i�A�F �W�I�C�h�j ���w�I�ɋߎ����� �i�C�F��]�ȉ~�́j ���߂Ēn���w�I�o�ܓx�̑���Ɋւ��鑪�ʂ̊�{�Ƃ��ėp���Ă��顂��� �i�C�F��]�ȉ~�́j �� �i�E�F�����ȉ~�́j�Ƃ����B �f�o�r���ʂŕW�������߂邽�߂ɂ́A�i�E�F�����ȉ~�́j ����n�\�܂ł̋����ł��� �i�G�F�ȉ~�̍��j�ɁA�i�E�F�����ȉ~�́j �����i�A�F �W�I�C�h�j�܂ł̋����ł����i�I�F�W�I�C�h���j������K�v������B �@����āA�ł��K���Ȍ��̑g�����́A�P�ł���B
�F�P |
|
<H20-2-B�F��>
���@�֘A���i�������ʁF�����p�̌v�Z�j No2�i���p���ʁj�F�iH4-B�j�EH20-B�i�o��@1�^15�j
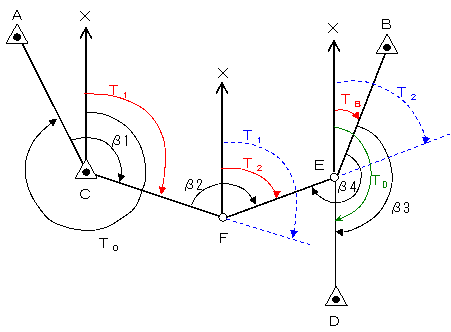
���̂悤�ɍl���A�v�Z����g�ݗ��Ă�B �@�O�}���A�d�_�ɂ�����A�_�c�̕����p�i�s�c�j�́A �@�s�c �� �s�a�{��3�@�@����@ �ɂ�苁�߂鎖���ł���B
�@�܂��A�d�_�ɂ�����a�_�̕����p�i�s�a�j�́A�����̂悤�ɋ��߂���B �@�s�P���i�s�O�{��1�j�|360�� �@�s�Q���i�s�P�{��2�j�|180�� �@�s�a���i�s�Q�{��E�j�|180���@�������ŁA��E �� 360���|��4 �@������܂Ƃ߂�ƁA���̂悤�ɂȂ�B �@�s�a �� �s�O�{��1�{��2�{��E�|720�� �@����ɐ��l�Ă͂߂�ƁA �@�s�a �� 332��15��10���{ 136��55��15���{ 139��23��40���{ �i360���| 227��05��10���j�|720�� �@�@ �� 21��28��55��
�@������@���ɑ������ƁA���̂悤�ɂȂ�B �@�s�c �� 21��28��55���{ 155��00��10���� 176��29��05��
����āA�d�_�ɂ�����A�_�c�̕����p�́A176��29��05���ƂȂ�B
�F�Q |
|
<H20-2-C�F��>
���@�֘A���i���g�����V�̌덷�j No2�i���p���ʁj�FH10-A�EH12-A�EH13-A�EH14-A�EH17-A� H18-B�EH19-C�EH20-C �i�o��@8�^15�j �@�� ���A�I���� 1. 2. �Ɋւ��ẮAH1�N�̎m�ŏo�肳�ꂽ��������B �� ���@�� �@���g�����V�̌덷�Ɋւ�����ł���B ���g�����V�ɂ�鋗������̌덷�́A���\�̂悤�ɑ��苗���ɔ�Ⴗ����̂ƁA���Ȃ����̂ɑ�ʂ����B��蕶���̂��`���̊e�덷�ɂ��čl����Ǝ��̂悤�ɂȂ�B
�@�ȉ��ɁA���e���ɂ��Č���Ǝ��̂悤�ɂȂ�B
�� �� �� ��
���r�F���g�����V�̗̍p���Ă���W�����ܗ��i�P�{���r�j �� �F�C�ۊϑ����瓾��ꂽ���ܗ��i�P�{�����j�@ ���ɁA�����͋ߎ��I�Ɏ��̎��ɂ��^������B
��蕶�́A�u���苗���v���ǂ��Ȃ�̂����Ă��邽�߁A�@����ό`���āA �@���ɖ�蕶�ɂ���悤�ɁA�C���ƋC���ɂ��čl����B
����āA�I�����u�Q�v���������B
�F�Q |
|
<H20-2-D�F��>
���@�֘A���i�ΐS��v�Z�F�]���藝�j No2�i���p���ʁj�FH6-A�EH9-C�EH20-D�i�o��@3�^15�j
�@ �@ ���̎��ɐ��l��������B �@
����āA�����r�́A�R�� 980.612�� �ƂȂ�B
�F�R
|