<H19-2-A：解答>

●　関連問題（測量の基準）

No2（多角測量）：H19-A

No1（三角測量）：H15-D・H16-C（出題回数　3／16）

●解　答

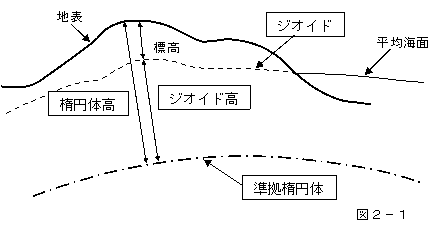
　測量の基準（標高）に関する問題である。
 

　地球上を全て海面として考えた場合の平均的な高さ（平均海面）をジオイドと称しているが、このジオイドは、完全な楕円体ではなく凹凸があるため、測量の基準として考えるのは適当ではない。　　　

そこで、ジオイドに近似した回転楕円体を定めて地球の形状や大きさを定めている。これを準拠楕円体と言う。

　日本ではこの準拠楕円体として、世界各国で用いられているＧＲＳ80楕円体を測量法にて採用しており、これを世界測地系と言う。また高さについては、東京湾平均海面（ジオイド）からの高さを基準として定めている。
　問題文にある図に、語句をあてはめると次のようになる。これにより、各基準面と標高の関係が理解できる。

　よって、最も適当な語句の組合せは、５である。
 

解答：５

<H19-2-B：解答>

●　関連問題（多角計算：座標の計算）
　　No2（多角測量）：H4-B・H5-D・H12-C・H15-C・H19-B（出題回数　5／16）

●解　答

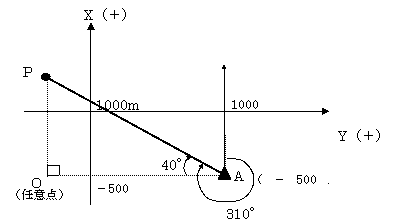
　座標計算に関する問題である。
　問題文を図にまとめると次のようになる。




　これより、点Ｐの座標位置は、点Ａから点Ｐに対する方向角より角ＰＡＸを求め、任意点Ｏを含めた、三角形ＰＡＯより三角関数によって計算すればよい事がわかる。

まず、∠ＰＡＯ ＝ 310°− 270°＝ 40°

次に、三角形ＰＡＯにおける、辺ＯＰ・ＯＡの長さは三角関数を用いて計算すると、

となる。※sinとcosの数値は、三角関数表より

問題文にある、Ａ点の座標値を元にＰ点の座標値を考えると次のようになる。

�]座標 ＝ − 500 ｍ ＋ 642.79 ｍ ＝ 142.79 ｍ
Ｙ座標 ＝ ＋1000 ｍ − 766.04 ｍ ＝ 233.96 ｍ

よって、点Ｐの座標値は、２の（ 142.79 ，233.96 ）となる。 

解答：２

<H19-2-C：解答>

●　関連問題（光波測距儀の誤差）

No2（多角測量）：H4-C・H5-C・H10-A・H12-A・H13-A・H14-A・H17-A･ H18-B・H19-C

（出題回数　9／16）

●解　答
　光波測距儀の誤差に関する問題である。
　光波測距儀による距離測定の誤差は、次表のように測定距離に比例するものと、しないものに大別される。問題文中のａ〜ｅの各誤差について考えると次のようになる。

ａ．器械定数の誤差　（測定距離に比例しない）
　光波測距儀に限らず器械はその製造過程から、必ず独自の誤差を持っている。このような器械独自の誤差を器械定数誤差と言い、その大きさを、「器械定数」として表している。器械定数は器械独自の一定の誤差であるため、測定距離には比例しない。

ｂ．反射鏡定数の誤差（測定距離に比例しない）
　プリズムは光波測距儀から発射された光を反射させる役割を持っているが、光波測距儀の器械定数同様に、個々の独自の誤差を持っている。この誤差は、プリズム定数（反射鏡定数）とも呼ばれ、測定距離に比例しない。

ｃ．気象要素の測定誤差（測定距離に比例する）
　光は空気中を通過するため、気象条件（気温、気圧、湿度）による影響により、光の速度が変化し誤差を生じてしまう。このような誤差を「気象誤差」と言い、当然、光が空気中を長く進めばその影響は大きくなり、測定距離に比例することがわかる。

ｄ．位相差測定の誤差（測定距離に比例しない）
　光波測距儀は、まず光を波に変えその波の長さ（波長）と、プリズムにより反射され光波測距儀に戻ったときに生じる、「波のズレの量」（位相差）を測定し計算により距離を測定する仕組みである。「位相差測定誤差」とは、この位相差を光波測距儀が測定するときに生じる誤差であり、その大きさは観測距離に関係なく器械によって異なる。このため、測定距離には比例しない。

ｅ．変調周波数の誤差（測定距離に比例する）
　光波測距儀により放たれる光は、実際はその発光時に一定の周波数で強弱を与えた（振幅変調）「波」として用いられている。光に強弱（振幅変調）を与える周波数は「変調周波数」と呼ばれ、光波測距儀内部にある基準発振器から発射されている。
　変調周波数の誤差とは、この基準発振器による基準周波数の誤差であり、これにより光の波長が変化するため、観測誤差が生じる。
　この誤差は、測定距離が長くなれば大きくなる、つまり測定距離に比例するものである。

よって、５のｃ，ｅの組合せが正しい。

解答：５

<H19-2-D：解答>

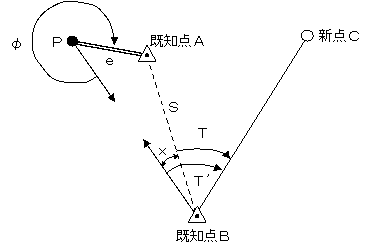
●　関連問題（偏心補正計算：正弦定理）
No1（三角測量）：H4-C・H5-D・H13-C・H14-C・H17-C
No2（多角測量）：H7-D・H8-D・H10-C・H16-C･ H19-D（出題回数　10／16）

●解　答

　偏心補正計算（正弦定理）の計算問題である。

 
　問題文より、水平角Ｔ＝Ｔ´−∠ＡＢＰ（ｘ）であることがわかる。∠ＡＢＰを求めるには、以下の手順で解いて行けばよい。

�@偏心補正計算により、偏心補正量�I′( ∠ＡＢＰ)を求める。

　＝  3′20″

ここで、sin330°は360°−330°として、sin30°で関数表によりその値を求めればよい。

※本来はsin330°＝−0.5として符号そのままにＴ´に加えればよい。ここでは、手計算であることを考慮して、あえてＴ＝Ｔ´−∠ＡＢＰの式を作成し、偏心補正角を＋の記号で算出している。

�AＴ＝Ｔ´−∠ＡＢＰ　により求める。

Ｔ＝ 42°55′20″− 3′20″＝ 42°52′00″

　よって、水平角Ｔは、３の42°52′00″となる。

解答：３