<H16-2-A:問題>

次の文は、標準的な公共測量作業規程に基づいて実施するGPS測量機を用いた測量について述べたものである。明らかに間違っているものはどれか。次の中から選べ。

１．GPS衛星を同時に3つ使用することができれば、基線解析を行うことができる。

２．観測点の近くに強い電波を発する構造物があると、観測精度が低下することがある。

３．基線解析では、観測点間の基線ベクトルが求められる。

４．基線解析における気象要素の補正は、基線解析ソフトウェアで採用している標準大気により行う。

５．基線解析で求められる観測点の高さは、楕円体高である。

<H16-2-A:解答>

１. GPS測量機により基準点測量を実施するためには、測位点の座標（x，y，z）と時計の誤差（⊿ｔ）の４つの未知数を解くため、４個以上のGPS衛星からの電波を同時に受信する必要がある。よって、問題文は明らかに間違いである。

２.問題文のように、障害電波発生源がある場所は、GPSアンテナの受信障害の原因となり、測位精度の低下を招く恐れがある。よって、問題文は正しい。

３.ＧＰＳ測量によって未知点の位置が求まるのは、既知点からの基線ベクトルが求まることにより、未知点の座標値が計算されるためである。よって、問題文は正しい。

４.気象要素の補正に用いる、気温、気圧及び湿度は、公共測量作業規程により「気象要素の補正は、基線解析ソフトウェアで採用している標準大気による」と定められている。よって、問題文は正しい。内で、搬送波の計算結果に補正している。

５.GPS衛星は地球中心（重心）の周りを回転しているため、GPS測量で求まる高さとは、地球中心を原点とした楕円体面から地上までの高さ、つまり楕円体高を求めていることになる。よって、問題文は正しい。

解答　１

<H16-2-B:問題>

求点Bの標高を求めるために、既知点A及び求点Bにおいてそれぞれ高低角及び斜距離Dの観測を行い、表2-1の結果を得た。求点Bの標高はいくらか。最も近いものを次の中から選べ。

ただし、斜距離Dは気象補正、器械定数補正及びミラー定数補正が行われているものとする。また、ジオイドの起伏、大気による屈折、地球の曲率は考えないものとする。

なお、関数の数値が必要な場合は、表2-2の値を使用すること。

 <H16-2-B:解答>

　①

ここで、ｈ_Ｂとｈ_Ａの計算について考えると、次のようになる。

よって、

この値を、①に代入すると、

となる。

※            正観測と反観測の計算は、別々に行い最後に平均をしても良いが、まとめたほうが計算しやすい。

※            両端から同時に観測を行うため、両差の影響は相殺される。

解答　４

<H16-2-C:問題>

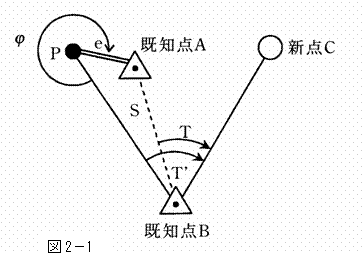
基準点測量において、既知点Aを基準に既知点Bから水平角を測定し新点Cの方向角を求めようとしたが、既知点Bから既知点Aへの視通が確保できなかったので、図2-1のように、既知点Aに目標の偏心点(P)を設けて観測を行い、表2-3の結果を得た。∠ABC(T)はいくらか。最も近いものを次の中から選べ。

ただし、既知点AB間の距離(S)は既知であり、1000.00mである。また、ρ″＝2″X10⁵とする。なお、関数の数値が必要な場合は、巻末の関数表を使用すること。

<H16-2-C:解答>

　この問題は、測点間距離が偏心点に対して対向する辺であるため、正弦定理を用いた偏心補正計算を行えばよい。

①  偏心補正計算により、偏心補正量ｘ（∠ABP ）を求める。

　 ＝ 5′0″

※偏心角αは、360°－ 330°により求まる。

②　∠PBC（T′）－X＝∠ABC（T）より、

　  46°35′0″－ 0°5′0″＝ 46°30′0″

よって、４が正しい。

解答　４

<H16-2-D:問題>

標準的な公共測量作業規程に基づいて、セオドライト(トランシット)と光波測距儀を用いて1級基準点測量を実施した。次のa～dは、この時の点検計算の工程を示したものである。標準的な計算の順序として、最も適当なものはどれか。次の中から選べ。

ただし、観測において少なくとも1点は、偏心点での観測があったものとする。

a.標高の点検計算をする。

b.座標の点検計算をする。

c.偏心補正計算をする。

d.基準面上の距離及びX・Y平面に投影された距離の計算をする。

１．ａ → ｃ → ｄ → ｂ

２．ａ → ｄ → ｃ → ｂ

３．ｄ → ｃ → ａ → ｂ

４．ｄ → ｃ → ｂ → ａ

５．ｃ → ｄ → ｂ → ａ

<H16-2-D:解答>

　点検計算の工程は次のようになる。

①ａ.標高の点検計算

②ｄ.基準面上の距離及びＸ・Ｙ平面に投影された距離の計算

③ｃ.偏心補正計算

④ｂ.座標の点検計算

　よって、ａ → ｄ → ｃ → ｂ　となり、解答は２になる。

解答：２

http://www.kinomise.com/sokuryo/　測量士・測量士補 試験対策WEB