<H16-1-A:問題>

次の文は、平成13年6月20日の測量法の改正(平成14年4月1日施行)及びこれに関連した法令等の改正により生じた変化について述べたものである。

明らかに間違っているものはどれか。次の中から選べ。

１.準拠楕円体が変更され、長半径と扁平率の値が変わった。

２.日本経緯度原点の経度、緯度の値が変わった。

３.全国の三角点について、平面直角座標のX座標、Y座標の値が変わった。

４.日本水準原点の標高が変わった。

５.平面直角座標系の各座標系原点について、地球上での位置が変わった。

＜H16-1-A：解答＞

　問題各文について見ると、次のようになる。

１．準拠楕円体はベッセルの楕円体から、GRS80楕円体に変更され、長半径・短半径・扁平率の値が変更された。よって、問題文は正しい。

２．世界測地系への移行に伴い、水平位置の基準である経緯度原点の値も下のように変更された。（経緯度差 -11秒6261　緯度差 11秒6424）よって、問題文は正しい。　

３．問題文の通り。経緯度原点（Ⅸ系）を例に取ると、経度が東に約12秒、緯度が南に約12秒移動しているため、その平面直角座標値は、Xで約+360ｍ、Yで約－300m移動した値となる。移動量は従来の成果におけるゆがみ等の補正のため、全国一律の値ではない。よって、問題文は正しい。

４．世界測地系になっても、高さの基準は変更されていないため、水準原点の標高が変わる事はない。問題文は明らかに間違いである。

５．測量法の改正において、平面直角座標系は原点の経度・緯度の数値、投影法、座標系の数、楕円体面上から平面への長さの縮尺係数及び適用範囲等について、これまでの定義を変えていない。このため、実際の位置（地球上の位置）が変わる事になる。よって、問題文は正しい。

解答：４

＜H16-1-B：問題＞

標準的な基準点測量の作業順序として最も適当なものはどれか。次の中から選べ。

ただし、a:踏査・選点　b:成果品の整理　c:観測　d:計画・準備　e:測量標の設置　f:平均計算とする。

１.       d　→　a　→　f　→　e　→　c　→　b

２.       d　→　e　→　a　→　f　→　c　→　b

３.       d　→　a　→　e　→　c　→　f　→　b

４.       d　→　a　→　e　→　f　→　c　→　b

５.       d　→　e　→　c　→　a　→　f　→　b

＜H16-1-B：解答＞

標準的な基準点測量の作業工程は、　「ｄ→ａ→ｅ→ｃ→ｆ→ｂ」の組合せとなる。よって、３の選択肢が正しい。

解答：３

＜H16-1-C：問題＞

次の文は標高、楕円体高、ジオイド高の関係について述べたものである。図1-1の模式図を参考にして 　ア　　～　　エ　  に入る語句の組合せとして正しいものを次の中から選べ。

　ア　 は平均海面に相当する面を陸地内部まで延長したときにできる仮想の面として定められたものである。図1-1に示すとおり、　イ　 は 　ア　 を基準として測定される。

　ア　 の形状は地表よりはなめらかであるが、地球内部の質量分布の不均質などによって凹凸がある。そのため、測量の基準面としては、　ア　 に適合するような回転楕円体面を、地球と関連づけたものを採用する。これを準拠楕円体という。この時、準拠楕円体から観測点までの高さを　

　ウ　、準拠楕円体から 　ア　までの高さを 　エ　 という。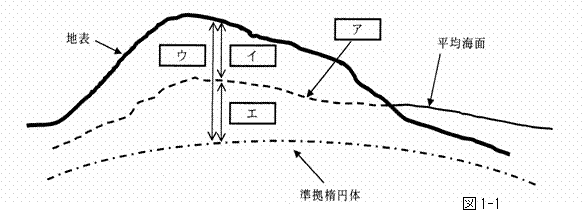

＜H16-1-C：解答＞

　問題文にある図に、語句をあてはめると次のようになる。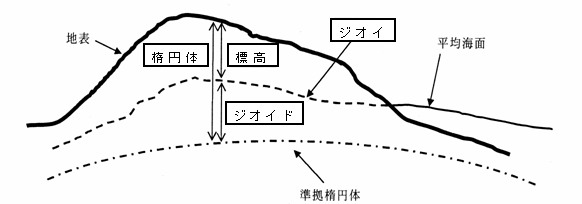

解答：３

＜H16-1-D：問題＞

1級基準点測量において、トータルステーションを用いてある水平角を2対回観測し、表1-1の結果を得た。この観測結果から求められる水平角の最確値はいくらか。最も近いものを次の中から選べ。

＜H16-1-D：解答＞

各対回における結果を求めると、次表のようになる。

※ 計算結果が－（ﾏｲﾅｽ）になる場合は、一回転したと考えて、＋360°をする。

次に、最確値を求める。（観測に対する「重量」がないため、単純平均でよい）

よって、最も近い値は「４」となる。

解答：４

※この問題において、観測結果の良否を問う、倍角差・観測差の検討を行うと、両値ともに許容範囲内であるため、再測の必要がないことがわかる。

http://www.kinomise.com/sokuryo/　測量士・測量士補 試験対策WEB