|
��No14�F�n�`���ʁF��
�@�������Ɋւ���v�Z���ł���B���̂悤�ɍl����Ηǂ��B
�@��蕶��}�ɕ`��
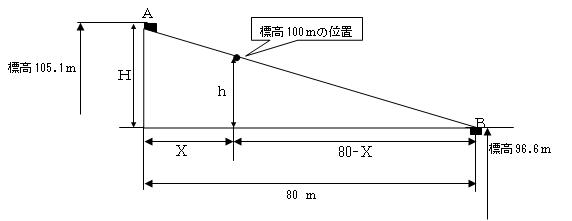
�A �`�E�a�_�̕W���������߂�
�@�@105.1�� �| 96.6�� �� 8.5��
�B�W��100���̈ʒu�����߂�
�@�����ŁA�_�`�`�a�����Ԑ���ŕW��100���̓������̈ʒu���l����ƁA�O�p�`�̑������A���̔�Ꭾ���g�ݗ��Ă���B
�@�_�`����W��100���̓������܂ł̍��፷�i���j�� �@105.1���|100���� 5.1���@����āA
�@8.5���@�F�@80���@���@5.1���@�F �w�@�ƂȂ�A����������ƁA
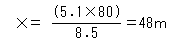
�ƂȂ�A�`�_����A48���̈ʒu�ɕW��100���̓�����������ƌ�����B
�C�n�}��̈ʒu�����߂�
�@�k�� 1�^1,000 �n�`�}��ŕ\���ƁA���̒n�`�}��̒����́A�@48�� �^ 1,000 �� 4.8 cm �ƂȂ�B
�@����āA1�^1,000 �n�`�}��ł́A�`�_����4.8cm�̈ʒu�ŁA�W��100���̓������Ƃ`�a�����Ԓ������H�Ƃ̌�_������B
����čł��߂��l�́A�Q �ƂȂ�B
|