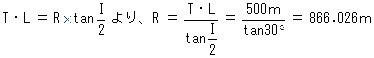＜No25：応用（路線）：解答＞

　路線測量における作業工程に関する問題である。正しい語句を当てはめると次のようになる。

よって、最も適当な組み合わせは２．となる。

解答：　２

＜No26：応用（路線）：解答＞

　単曲線設置に関する問題である。TLが現道路と新道路の共通項であることを利用して次のように考えればよい。

１．計画された単曲線の諸要素を基に、現道路のTL（BC〜IP）を計算する。

２．新道路の交角が60°となった場合の曲線半径（R）を求める。

※ ここで、TLの値が計画前後で変化しないことに着目する。

また、tan30°の値は、関数表より0.57735 とする。

３．新道路の曲線長（CL）の値を求める。




よって、一番近い選択肢４．が正答となる。

解答：　４

＜No27：応用（用地）：解答＞

　座標による面積計算に関する問題である。座標による面積計算はその計算手順を覚えておけば、簡単に解ける問題でもある。土地ABCDの面積を先に求め、それを手掛かりに次のように解答すれば良い。

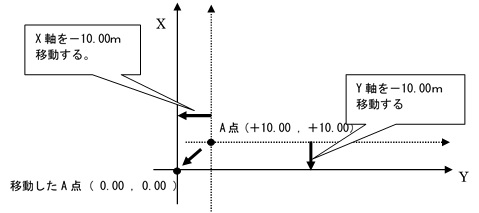
�@ 座標原点を移動し、座標値を計算しやすい数値にする。

※   問題で与えられた数値のまま計算を行っても良いが、士補試験では電卓の使用が禁止されているため計算ミスを引起す可能性がある。このため、上記のように座標を移動したと仮定して、下表のように簡単な数値に直してから計算を実行するのが良い。

�A 次のような計算表を作成し、数値を入れ倍面積、面積と計算する。

よって、境界杭  A，B，C，Dで囲まれた土地の面積は、2450.000 �u となる。

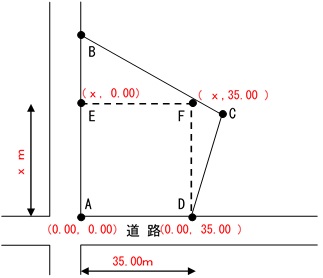
�B ここで問題の図を見ると、次のように考えられる。

求めるべき土地　A，E，F，Gは、問題文より長方形であるため、その面積は、35.00 ｍ × ｘ となる。また土地の面積が土地A,B,C,Dの60％であるため、�A で求めた面積を用いて、次の式を組み立てる。

（2450.00 �u ×0.6）＝ 35.00 ｍ × ｘ　　よって、ｘ ＝ 42.00 ｍ

ここで、�@ において、計算の都合上座標値を移動しているため、これを加えると次のようになる。

42.00 ＋ 10.00 ＝ 52.00

よって、点Fのｘ座標は、２の52.00 ｍとなる。

解答：　２

＜No28：応用（河川）：解答＞

　河川測量全般に関する問題である。問題各文について考えると次のようになる。

1.正しい。距離標設置測量に関する問題である。距離標は河心線の接線に対して直角方向に近傍の３級基準点等から放射法により左右両岸に設置される。

2.正しい。距離標設置測量に関する問題である。距離標は河心線に対して200ｍ間隔で左右両岸に設置される。

3.正しい。水準基標測量に関する問題である。水準基標は２級水準測量により行われ、設置間隔は、5〜20�qまでを標準とする。

4.正しい。定期縦断測量では、距離標の他に堤防の変化点や主要構造物について距離標からの距離と標高が測定される。

5.間違い。定期横断測量では、距離標ではなく水際杭を境として陸部と水部に分けられる。堤防法肩に設置される距離標ではない。

解答：　５