＜No25：応用（路線）：解答＞

　路線測量の図面類に関する問題である。問題各文について考えると次のようになる。

1.    正しい。線形決定にて作成される、線形図データファイルは、問題文のように計算により求めた主要点、中心点の座標値を用いて作成される。

2.    正しい。中心線測量により作成される、線形地形図は、問題文のように主要点及び中心点の座標値を地形図データに落として作成される。

3.    正しい。縦断測量により作成される縦断面図では、距離を表す横の縮尺は線形地形図の縮尺と同一とし、高さを表す縦の縮尺は、線形地形図の縮尺の5倍から10倍までを標準とする。

4.    間違い。横断測量により作成される横断面図の縮尺は、縦断面図の「縦」の縮尺と同一のものを標準とする。

5.    正しい。詳細測量により作成される、詳細平面図の地図情報レベルは問題文の通り250を標準とする。また、図紙に出力する場合は、縦断面図の横の縮尺は詳細平面図の縮尺と同一とし、縦の縮尺は100分の1を標準とする。また、横断面図の縮尺は縦断面図の縦の縮尺に合わせることを標準とする。

解答：　４

＜No26：応用（路線）：解答＞

　単曲線の計算に関する問題である。問題文のように弦長を求めるには、次のような手順で解答すればよい。

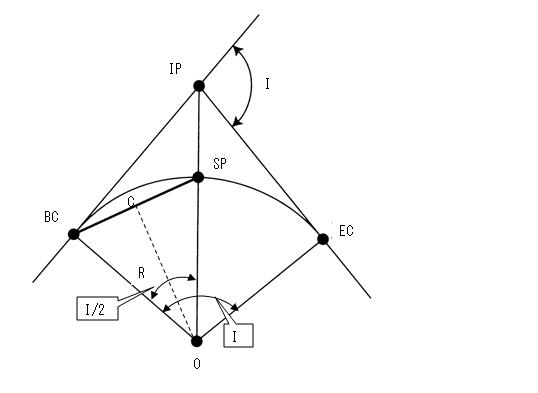
�@次図のように補助線O-Cを描き∠(BC-O-C)を求める。単曲線の特徴の１つとして、次のように交角（Ｉ）＝ ∠(BC-O-EC)また、∠(BC-O-SP) ＝ I/2となる。

　∠(BC-O-C)＝∠(C-O-SP) ＝ I/4 であるため、∠(BC-O-C)は　　108°÷ 4 ＝ 27° となる。

�A 弦長を求める。

弦長（BC-SP）は、直線(BC-C)×2であるため、三角形(BC-O-C)に注目して、三角関数により、直線(BC-C)を求めると、　R×sin(I/4) ＝ 100ｍ×sin27°＝ 45.399ｍ　となる。

よって、弦長(BC-SP)は、 45.399ｍ × 2 ＝ 90.798ｍとなり、最も近い値は、３の90.80ｍとなる。

解答：　３

＜No27：応用（用地）：解答＞

　座標法による面積計算に関する問題である。次の手順で解答すればよい。

�@問題文の座標値を簡単な数値に直す。

※特に不要と考えるようであれば、問題文の数字を用いれば良い。

�A計算表を作成し座標法により面積を求める。

　よって、点A,B,C,D で囲まれた土地の面積は、1,350 �u となる。

解答：　２

＜No28：応用（河川）：解答＞

　距離標設置測量に関する問題である。問題文に正しい語句を当てはめると次のようになる。

距離標の設置間隔は、河川の河口又は幹川への合流点に設けた起点から、河心に沿って 200ｍ
を標準とする。距離標は、図上で設定した距離標の座標値に基づいて、近傍の ３級 基準点等からトータルステーションによる 放射法 のほか、キネマティック法、RTK法又はネットワーク型RTK法により設置する。ネットワーク型RTK法による観測は、間接観測法又は 単点観測法 を用いる。

よって、正しい語句の組合せは、４ となる。

※幹川（かんせん）本流のこと。幹川に合流する川を支川（支流）と言う。

解答：　４