＜No13：地形測量：解答＞

　地形測量の細部測量に関する問題である。問題各文について考えると次のようになる。

1.    正しい。問題文の通り。TS等とGNSS測量機は併用もできる。

2.    正しい。問題文の通り。放射法で測定が行われ、観測は干渉測位方式で１セットで行われる。

3.    正しい。問題文の通り。ネットワーク型もキネマティック法又はRTK法も問題文のように行われる。

4.    正しい。問題文の通り。GNSS測量の特徴を述べている。

5.    間違い。GLONASS衛星を用いて観測する場合は、使用衛星数は6衛星以上とし、GPS及びGLONASS衛星を、それぞれ２衛星以上用いる必要がある。

　よって、明らかに間違っている文章は ５ となる。

解答：　５

＜No14：地形測量：解答＞

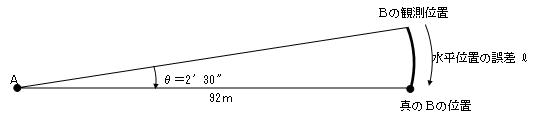
　角度のズレと水平距離で水平位置の誤差を求める問題である。次のように考えれば良い。

�@問題文を図に描く

�A ラジアンを用いて計算

　 


＝ 69�o となる。

※三角関数を用いた計算では次のようになる。

　ℓ＝ 92ｍ×sin 0°02′30″ ＝ 0.0669ｍ ≒ 70�o

　よって、点Ｂの水平位置の誤差は、69�oとなる。

解答：　５

＜No15：地形測量：解答＞

　等高線に関する計算問題である。次のように考えれば良い。

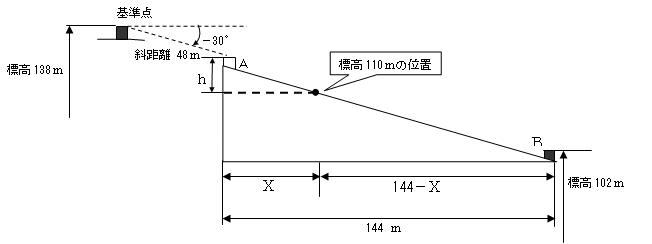
�@問題文を図に描く

�A Ａ点の標高を求める

　Ａ点の標高（ＨA）は、問題文より次のように求められる。

　138ｍ−48ｍ×sin30°＝ 114ｍ

�B標高110ｍの位置を求める

　ここで、点Ａ〜Ｂを結ぶ線上で標高110ｍの等高線の位置を考えると、三角形の相似より、次の比例式が組み立てられる。

　ＡＢ間の高低差は、114ｍ−102ｍ＝12ｍ、図中のｈは、114ｍ − 110ｍ ＝ 4ｍ　よって、

　4ｍ　：　Ｘ　＝　12ｍ　：144ｍ　となり、これを解くと、

となり、Ａ点から、　48ｍの位置に標高110ｍの等高線があると言える。

よって、Ｂ点からは、144ｍ−48ｍ ＝ 96ｍ　の位置にある。

�C地図上の位置を求める

　縮尺 1／1,000 地形図上で表すと、その地形図上の長さは、　96ｍ ／ 1,000 ＝ 9.6 cm となる。

　よって、1／1,000 地形図上では、Ｂ点から9.6cmの位置で、標高110ｍの等高線とＡＢを結ぶ直線道路との交点がある。

よって最も近い値は、５ となる。

解答：　５