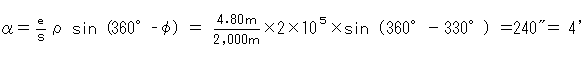＜No4：基準点測量：解答＞

　TSを用いた、基準点測量の点検計算に関する問題である。

　点検計算とはいわゆる現地計算の事であり、観測終了後に観測値に対する補正計算を行い、点検路線を選定し、許容範囲内の観測値であるか否かを判定するものである。以下に、問題各文について解説する。

1.    正しい。閉合差を求めるため、既知点と既知点を結合させる必要がある。

2.    間違い。点検路線を長くすると、再測を必要とする区間の判別が付きにくい。このため、点検路線はなるべく短いものとする必要がある。

3.    正しい。各既知点間の閉合差を求める必要があるため、１つ以上の点検路線で結合させる必要がある。

4.    正しい。再測を必要とする区間を判別するため、路線の１つ以上を重複させる必要がある。

5.    正しい。当然、許容範囲を超える区間は再測を行う必要がある。

　よって、明らかに間違っているのは２．の問題文となる。

解答：　２

＜No5：基準点測量：解答＞

　基準点測量の一般事項に関する問題である。ア〜エに入る語句を考えると、次のようになる。

選点とは、平均計画図に基づき、現地において既知点の現況を調査するとともに、新点の位置

を選定し、 　選点図及び平均図　 を作成する作業をいう。

新点の位置には、原則として永久標識を設置する。また、永久標識には、必要に応じ 　固有番号　 などを記録したＩＣタグを取り付けることができる。

トータルステーション（以下「TS」という｡）を用いる観測では、水平角観測、鉛直角観測及び距

離測定は、１視準で同時に行うことを原則とする。また、距離測定は、１視準 　２読定　 を１セットとする。

TSを用いた観測における点検計算は、観測終了後に行うものとする。また、選定されたすべての点検路線について､水平位置及び標高の 　閉合差　 を計算し、観測値の良否を判定するものとする。

ア：選点図及び平均図：選点作業に関する文章である。

イ：固有番号：永久標識（測量標）の設置に関する文章である。永久標識には規格及び設置方法が定められている。

ウ：２読定：観測作業に関する文章である。水平及び鉛直角観測は、１視準１読定、望遠鏡正反の観測を１対回としている。

エ：閉合差：点検計算に関する文章である。TSによる基準点測量の許容範囲は、水平位置も標高も全て閉合差で表される。

　よって、正しい選択肢の組合せは、５．となる。

解答：　５

＜No6：基準点測量：解答＞

　偏心補正計算（正弦定理）に関する問題である。次の手順で解答すればよい。

　問題の図より、Ｔ＝Ｔ’−∠ＡＢＰとなる。ここで、∠ＡＢＰ＝α　とすると、αは偏心計算により、次のように解く事ができる。

　よって、

　Ｔ＝45°37’00”− 4’＝ 45°33’00”　となる。

解答：　４

＜No7：基準点測量：解答＞

　GNSS測量の一般事項に関する問題である。問題各文について考えると次のようになる。

1.    正しい。スタティック法及び、短縮スタティック法による基線解析では、原則としてPCV補正※を行う必要がある。
従来は、「同一セッション、同一機種」が原則であったGNSS測量であるが、電子基準点等の利用が進み、異機種間のデータ解析を行う必要が出てきた。そこで、現在ではPCV補正を行う事により、異機種間のアンテナ位相特性を吸収し精度確保ができるようにしたものである。
※PCV（Phase Center Variation）：アンテナ位相特性とも呼ばれる。エポック（干渉測位でのデータ取得間隔）ごとにGNSS衛星からの電波の入射角に応じて受信位置が変化すること。これを補正する事をPCV補正と呼ぶ。従来はアンテナ定数による補正を行っていた。

2.    正しい。FIX解とは厳密解の事で、これが基線解析の結果となる。FIX解の対義語でフロート解（推定解）がある。

3.    正しい。GNSS観測では、片寄った配置のGNSS衛星を使用すると精度が低下するため、事前に衛星配置をアルマナックデータ（衛星の軌道情報）で確認する必要がある。衛星配置は、4つの衛星が造る四面体の体積が最大になる配置が良いとしている。

4.    間違い。マルチパス（多重反射）とは、建物や工作物、地面などにより衛星電波が乱反射し、GNSSアンテナがこれを受信する現象であり、GNSS測量における誤差原因の１つである。アンテナ高の統一と何ら関係は無い。

5.    正しい。GNSS測量とは衛星からの電波を受信して行うものである。このため、電波障害となる、電波発信源の近傍での観測は避けるべきである。

　よって、明らかに間違っているのは４．である。

解答：　４

＜No8：基準点測量：解答＞

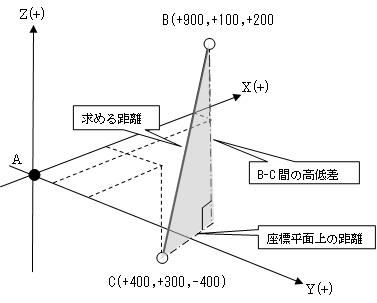
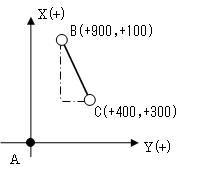
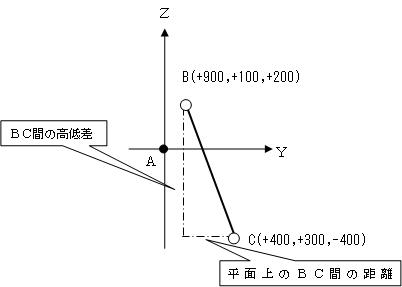
　座標計算に関する問題である。特に測量の知識を必要とするものではないが、座標軸（X,Y）が数学座標と逆であることに注意する必要がある。内容としては難しいものではなく、三平方の定理（ピタゴラスの定理）を用いて丁寧に解いて行けばよい。

　まず、問題文を図に描くと次のようになる。この際、問題として与えられている座標値がＡ点からの基線ベクトル成分（Ａ点を座標原点とした相対座標）である事に注意する。

　次に三平方の定理を用いて、座標平面上のＢ−Ｃ間の距離を求める。




最後に、�凾yの高低差とＢ−Ｃ間の座標平面上の距離を用いて、Ｂ−Ｃ間の斜距離を求める。

よって、Ｂ−Ｃ間の斜距離は、806.225ｍとなり、最も近いものは、３．806.226ｍとなる。 

解答：３