＜No25：応用（路線）：解答＞

　路線測量における各作業工程の内容に関する問題である。問題各文について考えると次のようになる。

1.    正しい。問題文の通りである。路線選定（ペーパーロケーション）とは、自然や生活環境等の制約、条件に合致するように道路計画を行ったものである。線形決定はこれを基に、主要点（IP）や中心点の座標値を求める作業である。

2.    正しい。問題文の通り。主要点には役杭を中心点には中心杭を設置する。

3.    正しい。問題文の通り。縦断測量は、中心杭高及び中心点並びに中心線上の地形変化点の地盤高及び中心線上の主要な構造物の標高を、平地においては４級水準測量、山地においては簡易水準測量により行うものである。

4.    正しい。問題文の通り。横断測量は、中心点における中心線の接線に対して直角方向の線上にある地形の変化点及び地物について、中心点からの距離及び地盤高を測定するものである。

5.    間違い。詳細測量とは、主要な構造物（橋梁やトンネル、擁壁など）の設計に必要な詳細平面図データファイル、縦断面図データファイル及び横断面図データファイルを作成する作業である。

解答：　５

＜No26：応用（路線）：解答＞

　水準測量における器高式野帳の記入方法に関する問題である。次の考え方で解けばよい。

１．補正量（イ）の計算 

　問題文の観測手簿から観測時のレベルの位置を考えると次図のようになる。

ここで、BM1とBM2の閉合差を求めると、ΣBS−ΣFS（TP）より、次のようになる。

　※赤字（後視：BS）、青字（前視：FS）

　(1.308＋0.841＋1.329＋1.042)−(1.043＋1.585＋0.646＋1.539)＝4.520−4.813＝−0.293ｍ

　ここで、BM1の標高を基に考えるとBM2の観測標高は、80.275ｍ−0.293ｍ＝79.982ｍ となる。

　BM2の決定標高は問題文の表より、79.985ｍであるため、BM1とBM2の閉合差は、次のようになる。

　79.985ｍ−79.982ｍ＝0.003ｍ　（3�o不足）

　よって、この閉合差を観測距離に応じて、前視の部分に補正すればよい。

　各区間の補正量は次のようになる。

　ここで問題文から1�o 単位の補正量であり、BM1 〜 No.1 の区間は、BM1を後視としているため、誤差が出にくいであろうと想定して、補正量を0�o とする。よって、（イ）には、「0」が入る。

２．（ウ）の計算

　標高は、（器械高）−（前視）＋（補正量）であるため、 81.583 − 1.043 ＋ 0 ＝ 80.540ｍ

　となる。

３．（ア）の計算

器械高は、（標高）＋（後視）であるため、80.540＋0.841＝ 81.381ｍ　となる。

よって、ア：81.381　　イ：0　　ウ：80.540　　となり、１が正答の組合せとなる。

解答：　１

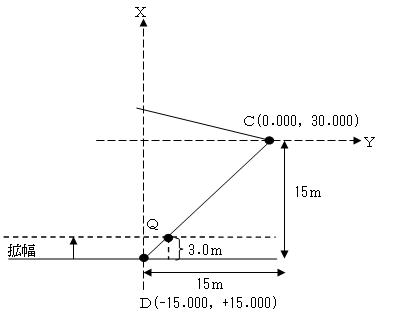
＜No27：応用（用地）：解答＞

　座標法による面積計算の問題である。次のように解答すればよい。

１．道路拡幅後の座標値を求める。

　Ａ→Ｐ座標（−12.000，−33.000）

　Ｄ→Ｑ座標（−12.000，＋18.000）

　※Ｄ→Ｑ座標移動した場合、次図よりＱの座標値は(-12.000，+18.000)となる。

２．座標法により面積を求める

　よって、点P,B,C,Q で囲まれた土地の面積は、1,219.50�u となる。

解答：　２

＜No28：応用（河川）：解答＞

　平均河床高を求める問題である。次のように考えれば良い。

　※平均河床高：通常時に河の水が流れる場所の河床の平均高さ。河川管理に用いられ、平均河床高が前回の高さより高ければ「堆積」、低ければ「浸食」している事を表す。

まず、問題文の図に数値を書き加えると次のようになる。

平均河床高は、上図を参考に図の網掛部の面積を求め、川幅で割って求めればよい。

１．問題文より、各測点間の勾配が一定であるため、河床部の面積を求める。

Ａ（三角形） ＝ ((6.2−4.7）×3)／2 ＝ 2.25 �u

Ｂ（台　形） ＝ (((6.2−4.7)＋(6.7−4.7))×2）／2 ＝ 3.50 �u

Ｃ（台　形） ＝ (((6.7−4.7)＋(6.7−4.7))×2）／2 ＝ 3.50 �u

Ｄ（三角形） ＝ ((6.2−4.7）×3)／2 ＝ 2.25 �u

よって、河床部の面積は、2.25＋3.50＋3.50＋2.25 ＝ 11.5 �u

２．河床部の平均標高を求める。

河床部の平均高は、次のように求められる。11.5 �u ／(3＋2＋2＋3) ＝ 1.15ｍ

河床部の平均標高は、次のようになる。　20.7ｍ＋(-4.7ｍ＋(-1.15ｍ)）＝ 14.85ｍ

よって、最も近いものは、3．の14.9ｍ　となる。

解答：　３