＜No4：基準：解答＞

　基準点測量（結合多角方式又は単路線方式）においてＴＳを用いた場合の一般的な事項に関する問題である。

各問題文について解説すると次のようになる。

1.正しい。
結合多角方式における多角網において、新点の位置精度は網の図形と観測量、観測精度によって決定される。作業規程の準則では、新点の精度確保のため、形成される図形の辺数や路線長、既知点数など一定の基準を設けている。その中で路線図形においても、新点と既知点を結ぶ角度や内側の夾角が定められている。

2.正しい。
角の観測には、水平角と鉛直角がある。水平角の観測値の点検においては、倍角差と観測差の点検。鉛直角の観測値の点検では、高度定数の較差の点検を行う必要がある。

3.間違い。
観測後の点検計算では、全ての単位多角形及び点検路線において水平位置と標高の閉合差を点検する必要がある。その点検路線は、次のような条件を満たす必要がある。①既知点と既知点の結合。②なるべく短い路線。③全ての既知点を1つ以上の点検路線で結合。④点検路線を重複させる。
　よって問題文のように、なるべく多くの辺を採用し、最長の路線を採用するのは間違いである。

4.正しい。
ＴＳによる観測終了後の点検計算では、問題文のように水平位置と標高の閉合差を計算し、観測値の良否を判断する。

5.正しい。
観測に使用するＴＳの点検は、観測着手前及び観測期間中に適宜行い、必要に応じて機器の調整を行うものとする。また、水平角、鉛直角、測距部のそれぞれが許容範囲内にあるか否かを点検する必要がある。

解答：　３

＜No5：基準：解答＞

　高低角（高度角）と高度定数の較差について求める問題である。次のように計算すればよい。

＜点Ａ＞

　ｒ－ℓ＝2Ｚ より、

　63°19′27″＋（360°－296°40′35″）＝126°38′52″

※   計算結果は常にマイナスのため、あらかじめ ℓ に360°を加えておく。

　よって、Ｚ＝128°38′52″／ 2 ＝63°19′26″

　ここで、高度角（α）は、水平線を基準として示す目標までの角度であるため、α＝90°－Ｚ で表される。

　よって、α＝90°－ 63°19′26″＝ ＋26°40′34″（仰角）　となる。

＜点Ｂ＞

　点Ａと同様に計算を行えば、

　40°35′12″＋（360°－319°24′46″）＝ 81°10′26″

　Ｚ＝81°10′26″／ 2 ＝ 40°35′13″

　α＝90°－ 40°35′13″＝ ＋49°24′47″

＜高度定数の較差の計算＞

高度定数の較差とは、各方向の高度定数の最大値と最小値の差であるから、

（360°0′2″－360°）－（ 359°59′58″－360°）＝ 4″

　となる。

※   高度定数：同一視準点のｒ＋ℓ（正反観測値の和）－ 360°で表わされる値。高度角（α）の大小に係わらず、一定の値を表わすため、観測値の良否の点検に用いられる。

　よって、最も正しい値の組合せは、４ となる。

解答：４

＜No6：基準：解答＞

多角測量における方向角の計算問題である。決して難しいものではなく、次図のように図中に補助線を加えて順序良く計算すれば解くことができる。公式を覚えるよりは、図を描き解けるようにした方が良い。

図より、新点(3)における既知点Ｂへの方向角（α3）を求めるには、α_Ａから順番に方向角を求めればよい。

・Ａ点における(1)への方向角

　α_Ａ＝（Ｔ_Ａ＋β_１）－360°＝ （330°14′20″＋ 80°20′32″）－ 360°＝  50°34′52″

・(1)点における(2)への方向角

　α1＝（α_Ａ＋β_２）－180°＝ （ 50°34′52″＋ 260°55′18″）－ 180°＝ 131°30′10″

・(2)点における（3）への方向角

α2＝（α1＋β_３）－180°＝ （ 131°30′10″＋ 91°34′20″）－ 180°＝  43°04′30″

・(3)点におけるＢへの方向角

　α3＋β_４－180°＝α2　であるため、

α2＝α3－β_４＋180°＝ 43°04′30″－ 99°14′16″＋ 180°＝ 123°50′14″

※各方向角とも、図を参照して式を導きだすのが基本である。

よって、新点(３)における、既知点Ｂの方向角は、123°50′14″となる。

解答：１

＜No7：基準：解答＞

GNSS測量に関する、運用と観測上の注意点等に関する問題である。基本的に旧GPS測量と何ら変わりはない。

　問題各文について解説すると、以下の通りである。

1.    正しい。
GNSSの定義に関する文章である。GNSSとは（Global Navigation Satellite Systems）全地球衛星測位システムの略称であり、作業規程の準則では「ＧＰＳ、ＧＬＯＮＡＳＳ及び準天頂衛星システムを適用する。」とある。また、GLONASS（グロナス）とはロシアのシステム。準天頂衛星システムとは日本のシステムである。

2.    間違い。
公共測量のGNSS測量では、基線ベクトルを得るために最低４機の測位衛星からの電波を同時に受信する必要がある。（GLONASSを併用する場合は５機）

3.    正しい。
衛星からの電波を受信して、２地点間の基線ベクトル（距離と方向）を求めるシステムのため、見通しは不要である。

4.    正しい。
観測点近辺にレーダーや電波塔など、障害電波発生源がある場所はGNSSアンテナの受信障害の原因となる可能性があるため、その使用を避けるべきである。障害電波発生源とは電気火花（高圧電線、電車線路、雷）・強力電波（レーダー、ラジオ等の放送局）・特定周波数電波（特定のGNSS受信機に影響・無線通信設備、携帯電話等）である。

5.    正しい。
GNSS衛星が発信する電波（搬送波）には、衛星の位置を計算するための軌道情報や時刻などの「航法メッセージ」と、観測に用いる周波である「Ｃ／ＡコードやＰコード」が含まれている。軌道情報が無ければ、衛星の位置が解らず、基線解析が行えない。

解答：２

＜No8：基準：解答＞

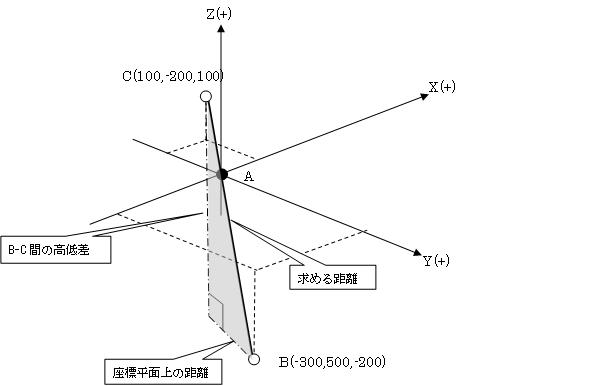
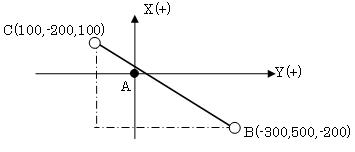
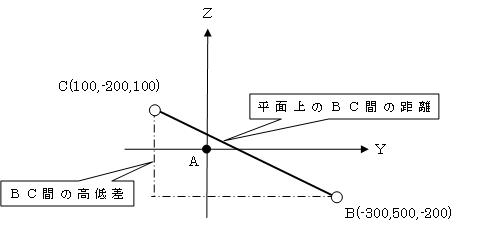
座標計算に関する問題である。特に測量の知識を必要とするものではないが、座標軸（X,Y）が数学座標と逆であることに注意する必要がある。内容としては難しいものではなく、三平方の定理（ピタゴラスの定理）を用いて丁寧に解いて行けばよい。

　まず、問題文を図に描くと次のようになる。この際、問題として与えられている座標値がＡ天からの基線ベクトル成分（Ａ点を座標原点とした相対座標）である事に注意する。

次に三平方の定理を用いて、座標平面上のＢ－Ｃ間の距離を求める。




最後に、⊿Ｚの高低差とＢ－Ｃ間の座標平面上の距離を用いて、Ｂ－Ｃ間の斜距離を求める。

よって、Ｂ－Ｃ間の斜距離は、860.233ｍとなる。

解答：４