| - PR - |
| - PR - |
| - PR - |
|
��No25�F���p�F�H���F��
�@�s�r��p�����A�Ԑڐ������ʂ̈�ł���u�Εӑ��ʁv�Ɋւ�����ł���B��ʓI�ɂ́A�s�r�̓����v�Z�@�\��p���ĂQ�_�Ԃ̍��፷�����߂邪�A�Q�_�Ԃ̃v���Y���i��B�j���������łȂ��ꍇ�ɂ́A���̊�B�����l������K�v������B �@���̉菇�Ƃ��ẮA�}�ɐ��l�������݂s�r�̊�B������Ƃ��āA�a�_�̕W�������߂�悢�B
�@ �}�ɗ^����ꂽ���l�������ނƎ��̂悤�ɂȂ�B 
�A TS�̊�B���i���������j�����߂�Ǝ��̂悤�ɂȂ�B �@�i35.500���{1.500���j�| 35.000���~sin30�� �� 19.500��
�B �a�_�̃v���Y���i��B�j�������߁AH�Q�̕W���l�����߂�Ǝ��̂悤�ɂȂ�B �@19.500���{50.000���~sin45����54.856�� �@����āAB�_�̕W��H�Q�́A �@54.856���|1.400����53.456��
���O�p���̒l�́A���̍Ō�ɂ���O�p���\��p���ċ��߂�B
�F�@�T |
|
��No26�F���p�F�H���F��
�@�H�����ʂɂ����钆�S�����ʂɊւ�����ł���B���e���ɂ��čl����Ǝ��̂悤�ɂȂ�B
�F�@�Q |
|
��No27�F���p�F�p�n�F��
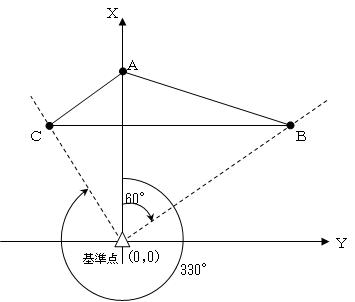
�@���W�@�ɂ��ʐόv�Z�Ɋւ�����ł��邪�A���̑O�ɁA�����p�Ƌ�����p���Ċe�_�̍��W�l�����߂��Ԃ�������B �@���̂悤�ɐ}��`���A���W�l�̕������l���Ȃ�������Ɨǂ��B
�@ �`�`�b�y�ъ�_�̊W�}��`���Ǝ��̂悤�ɂȂ�B
�A �����p�ƕ��ʋ�������`�`�b�_�̍��W�l�����߂�Ǝ��̂悤�ɂȂ�B ���`�_�̍��W�l�� �wA �� �{32.000���@�@�@�xA �� 0.000�A ���a�_�̍��W�l�� �@�@�@�wB �� 40���~cos60���� �{20.000���@�@�@�xB �� 40���~sin60���� �{34.641�� ���b�_�̍��W�l�� �@�@�@�wC �� 24���~cos30���� �{20.785���@�@�@�xC �� 24���~sin30�����|12.000�� ���O�}����ɁA�w�C�x�̕����ɒ��ӂ���B
�B ���W�@�ɂ��ʐόv�Z
�@����āA�O�p�`�`�C�a�C�b �̓y�n�̖ʐς́A266.250 �u�@�ƂȂ�B
�F�@�T
|
||||||||||||||||||||||||||||||
|
��No28�F���p�F�͐�F��
�@�͐쑪�ʑS�ʂɊւ�����ł���B���e���ɂ��čl����Ǝ��̂悤�ɂȂ�B
�F�@�S |