| - PR - |
| - PR - |
| - PR - |
|
��No4�F��_���ʁF�� GNSS�i�S�n���q���q�@�V�X�e���F��GPS�j���ʂ̊ϑ���@�⒍�ӓ_�Ɋւ�����ł���BH23�N�́u��p�K���̏����v�̉����ɂ��AGPS�q���i�A�����J�j��GLONASS�q���i���V�A�j�p���ė��p���鎖���ł���悤�ɂȂ������߁A�]����GPS���ʂ���GNSS���ʂւƖ��̂��ύX���ꂽ�B�]����GPS���ʂɊւ�������𗝉����Ă���Ή�������ł���B ��蕶�ɐ��������Ă͂߂�Ǝ��̂悤�ɂȂ�B
����āA�ł��K���Ȍ��̑g�����́A�P�ƂȂ�B �F�@�P |
|
��No5�F��_���ʁF��
�@No4�Ɠ��l�ɁAGNSS���ʂ̊ϑ���̒��ӓ_���Ɋւ�����ł���B��{�I��GPS���ʂƉ���ς��͂Ȃ��B �@���e���ɂ��ĉ������ƁA�ȉ��̒ʂ�ł���B
�F�@�T |
|
��No6�F��_���ʁF��
�@�ΐS��v�Z�i�����藝�j�̌v�Z���ł���B
��蕶���A�����p�s���s�L�|�ڂo�a�`�i���j�ł��邱�Ƃ��킩��B�ڂo�a�`�����߂�ɂ́A�ȉ��̎菇�ʼn����čs���悢�B
�@�@ �ΐS��v�Z�ɂ��A�ΐS����I��( �ڂo�a�`)�����߂�B �@ �����ŁAsin330����360���|330���Ƃ��āAsin30���Ŋ��\�ɂ�肻�̒l�����߂�悢�B �� �{����sin330�����|0.5�Ƃ��ĕ������̂܂܂ɂs�L�ɉ�����悢�B�����ł́A��v�Z�ł��邱�Ƃ��l�����āA�����Ăs���s�L�|�ڂo�a�`�̎����쐬���A�ΐS��p���{�̋L���ŎZ�o���Ă���B
�A�@�s���s�L�|�ڂo�a�`�@�ɂ�苁�߂�B �@ �s�� 83��20��30���| 900��(15��) �� 83��05��30��
�@����āA�����p�s�́A�S �ƂȂ�B
�F�S |
|
��No7�F��_���ʁF��
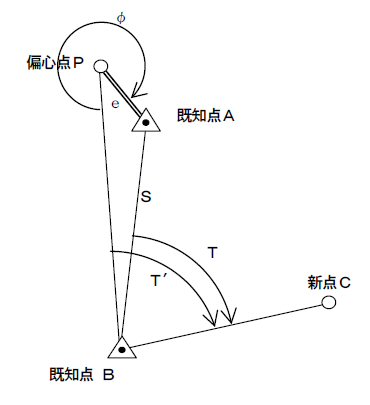
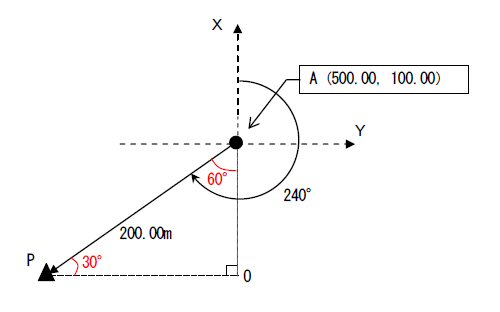
�@���W�v�Z�Ɋւ�����ł���B���ɑ��ʂ̒m����K�v�Ƃ�����̂ł͂Ȃ����A���W�������w���W�Ƌt�ł��邱�Ƃɒ��ӂ���K�v������B �@�܂��A��蕶��}�ɕ`���Ǝ��̂悤�ɂȂ�B �}���_�o�̍��W�ʒu�����߂邽�߂ɂ́A�_�`����_�o�ɑ�������p��p���āA�C�ӓ_�n���܂߂��O�p�`�o�`�n�̓��p�����߁A�O�p����p���Čv�Z����悢�B
�@�܂��A�ڂo�`�n �� 240���|180���� 60�� �@���ɁA�O�p�`�o�`�n�ɂ�����A�ӂn�o�E�n�`�̒��������߂�ƁA �n�o��200.00�� �~ sin60���� 200.00�� �~ 0.86603 �� 173.21�� �n�`��200.00�� �~ cos60���� 200.00�� �~ 0.50000 �� 100.00�� ��sin�Ecos�̒l�́A�O�p���\�ɂ��B �������́A�����p���w�C�x���W���Ƀ}�C�i�X�����ł���B
�@���ɁA��蕶���̂`�_�̍��W�l�ɂ����������ƁA�o�_�̍��W�l�ɂȂ�B �w���W �� �{500.00 �� �{ �|100.00�� �� �{400.00�� �x���W �� �{100.00 �� �{ �|173.21�� �� �| 73.21��
����āA�_�o�̍��W�l�́A�S�́i�{400.00�C�|73.21�j�ƂȂ�B
�F�S |
|
��No8�F��_���ʁF��
�@�g�����V�b�g�̌덷�Ə����@�Ɋւ�����ł���B���e���ɂ��āA�덷�Ə����@���l����Ǝ��̂悤�ɂȂ�B
����āA�]�����̐��E���̊ϑ��l�ς��Ă������ł��Ȃ��덷�̑g�����́A�Q�ƂȂ�B
�F�@�Q |