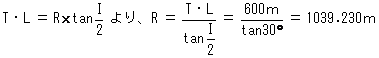| - PR - |
| - PR - |
| - PR - |
|
��No25�F���p���� �H���F��
�@�P�Ȑ��ݒu�Ɋւ�����ł���B�P�Ȑ��̐ݒu���́A�P�Ȑ��̌�����A�e���Y�iIP��BC�AEC�Ȃǁj�̈Ӗ�����������Ɗo���Ă����K�v������B������}�`�̖��ł����邽�߁A�ߋ�������������Ƃ��Ȃ��p�^�[���𗝉����Ă����Ƃ悢�B
�@���̂悤�ɁA�l���ĉ����Ηǂ��B �P�D�v�悳�ꂽ�P�Ȑ��̏��v�f����ɁAT�EL�iBC�`IP�j���v�Z����B �F�@�S |
|
��No26�F���p���� �p�n�F��
�� ���@�� �@��ԂƂȂ����A���W�@�ɂ��ʐόv�Z�̖��ł���B�����ē�����ł͂Ȃ��A�v�Z�\�̍��������o���Ă����Ή�����B�܂��A���ɗ^����ꂽ���W�l���ȒP�Ȑ��l�ɒ����Čv�Z����̂��A��@�ł���B
�ȉ��̎菇�ʼn���Ηǂ��B
�P�D���W���_���ړ����A���W�l���v�Z���₷�����l�ɂ���B ��1���ŗ^����ꂽ���l�̂܂܌v�Z���s���Ă��ǂ����A�m�⎎���ł͓d��̎g�p���֎~����Ă��邽�ߌv�Z�~�X��U������\��������B���̂��߁A��L�̂悤�ɍ��W���ړ������Ɖ��肵�āA���\�̂悤�ɊȒP�Ȑ��l�ɒ����Ă���v�Z�����s����̂��ǂ��B
��2���̖��Ɋւ��ẮA�����_�ȉ��̒l���Ȃ����߁A���ɕK�v�Ƃ��Ȃ����A���_���O�C�O�ł���A�v�Z������邽�߁A�����ā�1�̂悤�ɂ����B
�Q�D���̂悤�Ȍv�Z�\���쐬���A���l�����{�ʐρA�ʐςƌv�Z����B
����āA
���E�Y �`�C�a�C�b�C�c�ň͂܂ꂽ�y�n�̖ʐς́A�R �� 2,503�u �ƂȂ�B �F�@�R |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
��No27�F���p���� �p�n�F��
�p�n���ʂɂ�����e��Ɠ��e�Ɋւ�����ł���B��ʓI�Ȏ����Ȃ̂ō�ƍH���ƕ����āA���Њo���Ă��������B ��蕶�ɓK���Ȍ��Ă͂߂�ƁA���̂悤�ɂȂ�B
�@����āA���������̑g�ݍ��킹�́A�P�ƂȂ�B
�F�@�P |
|
��No28�F���p���� �͐�F��
�͐쑪�ʂɂ�����e��Ɠ��e�Ɋւ�����ł���B��ʓI�Ȏ����Ȃ̂ō�ƍH���ƕ����āA���Њo���Ă��������B ���e���ɂ��čl����Ǝ��̂悤�ɂȂ�B
�F�@�Q |