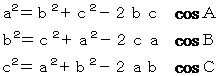| - PR - |
| - PR - |
| - PR - |
|
��No4�F��_���ʁF�� �@GPS�@���p������_���ʂɊւ�����ł���BH17�N�x�����肩��A��_���ʂɉ������I�������ڗ��悤�ɂȂ������A���̖����e�͌����ē�����̂ł͂Ȃ��AGPS���ʋ@�Ɋւ����b�I�����Ƃ����p�����ϑ���Ƃ̓��e�⒍�ӎ����Ɋւ�����̂ł���B ��ԂƂ���������ł��邽�߁A�ߋ������������Ɨ������A��������悤�ɂ��Ă��������B
�ȉ��A�e�I�����ɂ��ĉ������B
����āA���炩�ɊԈ���Ă���̂́A�P�ł���B
�F�P |
|
��No5�F��_���ʁF��
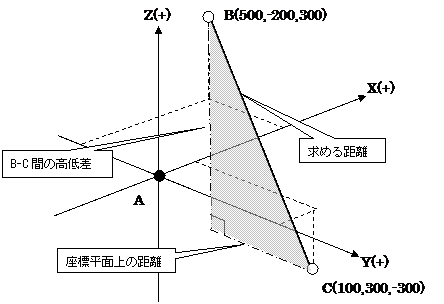
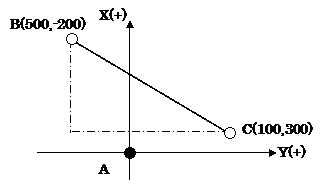
�@���W�v�Z�Ɋւ�����ł���B���ɑ��ʂ̒m����K�v�Ƃ�����̂ł͂Ȃ����A���W���iX,Y�j�����w���W�Ƌt�ł��邱�Ƃɒ��ӂ���K�v������B�܂��A���߂Ăy�����̍��W�i�����j���^�����A���W��Ԃ̌v�Z���v�����ꂽ�B���e�Ƃ��Ă͓�����̂ł͂Ȃ��A�O�����̒藝�i�s�^�S���X�̒藝�j��p���Ē��J�ɉ����čs���悢�B �@�܂��A��蕶��}�ɕ`���Ǝ��̂悤�ɂȂ�B
���ɎO�����̒藝��p���āA���W���ʏ�̂a�|�b�Ԃ̋��������߂�B
�F�R |
|
��No6��_���ʁF��
�@�g�[�^���X�e�[�V����(�ȉ��s�r)�ƃf�[�^�R���N�^�i�ȉ��c�b�j�̓����Ɋւ�����ł���B�������炭�̏o��͖����������A�o����e�i�I�����j��H18�Ƃقړ����ł���A�ȒP�ɉ�������ł���B �@�ȉ��A�e�I�����ɂ��ĉ������B
1.
�������B �@����āA���炩�ɊԈ���Ă���I�����́A�T�ƂȂ�B
�F�T |
|
��No7��_���ʁF��
�@��_���ʏ��i�\�j�Ɋւ�����ł���B�O�⓯�l�ɁA�������炭�̏o��͖����������A�o����e��H18�Ƃقړ����ł���A�ȒP�ɉ�������ł���B�k�ڌW�����v�Z�ɂ�苁�߂��Ƃ��A�����o����B ���� �A�`�E �ɂ��čl����ƁA���̂悤�ɂȂ�B
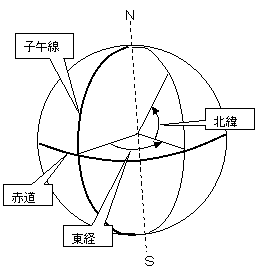
���A�E�C�� �@���ʏ��ɂ���O�p�_�̌o�ܓx�ƁA���ʒ��p���W�n�i�\�n�j�̍��W���_�̌o�ܓx���r����ƁA�ܓx�̓}�C�i�X�����A�o�x�̓v���X�����Ɉʒu���Ă��遦���Ƃ��킩��B����āA�A�ɂ́u�|�v�A�C�ɂ́u�{�v�̕���������B ���ܓx�F���_���W���A�쑤�Ɉʒu���Ă���B�i�ܓx�i�k�܁j�͖k�ɂ�90���j �@�o�x�F���_���W���A�����Ɉʒu���Ă���B�i�o�x�i���o�j�͍����ő����j
���E�� �@�C�Ӓn�_�̏k�ڌW���́A���̎��ɂ�苁�߂邱�Ƃ��ł���B �� �����O�{ �i�x�Q �^2�q�Q�E���O�Q�j �����ŁA���͔C�Ӓn�_�̏k�ڌW���A�x�͂x���W�l�ikm�P�ʁj�A�q�͒n���̔��a�i6,370km�j�A���O�́A0.9999��@���āA �� �� 0.9999 �{ �o14.5�Q �^�i2�~6370�Q�~0.9999�Q�j�p �� 0.999903 �@���̎O�p�_�̏k�ڌW���́A0.999903�ƂȂ�B
��
�����Ɍv�Z���s��Ȃ��Ƃ��A�����������Ȃ�Ύ��̂悤�ɍl����悢�B �F�S |
|
��No8��_���ʁF��
�@�ΐS��v�Z�i�]���藝�j�̌v�Z���ł���B��Ӛ�i���傤�j�p�ɂ��v�Z�Ƃ��Ă��B �@���̂悤�ɁA�]���藝��p���ĕΐS�_�ɑΌ�����ӂ̒��������߂�悢�B
�@���̎O�p�`�`�a�b�ɂ����āA���̊W�����藧�B
�@���̐}����A�]���藝��p���Ď���g�ݗ��Ă�ƁA���̂悤�ɂȂ�B �@ ���̎��ɐ��l��������B �@
�@����āA�����r�́A�R�� 854�� �ƂȂ�B
�F�R |