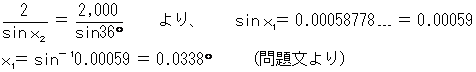| - PR - |
| - PR - |
| - PR - |
|
��No4�F��_���ʁF�� 1�D�������B
4�D�������B �@ GPS���ʂ́A�q������̓d�g����M���A���e�i�ʒu�̍��W�����߂鑪�ʕ��@�ł���B���R�A�q������̓d�g���Ւf������A��Q���N�������̋߂��͔�����ׂ��ł���B
5�D�ԈႢ�B �@ ���m�_�Ԃ����ԑ��p�H���́A�ߓ_����ӂ̐����ł��邾�����Ȃ��A�ߓ_�Ԃ̋������ł��邾���������A������ɕ��R�Ȍo�H��I������K�v������B����ɂ��ϑ������炵�ϑ��덷�̔��������������A�ϑ���Ƃɂ�����������グ�鎖���o����B �܂��A�ߓ_�Ƃ́A��Q�����ɂ��אڂ����_�Ԃ̌��ʂ����Ȃ��ꍇ�ɁA��ނ������݂����鉼�݂̊ϑ��_�i���p���_�j�ł���B�������ʍ�ƋK��ł́A��_���ʂ̋敪�i�P���`�S���j�ɂ����āA�ߓ_�Ԃ́i�Œ�j���������߂��Ă���B �F�T |
|
��No5�F��_���ʁF�� H16-2-D�EH21-5�i�o��@2�^16�j �@��_���ʂɂ�����_���v�Z�̍H���i�����j�Ɋւ�����ł���BH16�N�ȍ~�Q��ڂ̏o��ł��邪�A��_���ʂ̍�ƍH���Ɋ܂߂Ċo���Ă����Ƃ悢�B
�@��_���ʂł́A�ϑ���Ƃ��I������ƁA���n�ɂ����Ċϑ��l�̗ǔۂ����߂錻�n�v�Z���s���K�v������B���̌��n�v�Z�́A�傫���ϑ��l�ɑ����v�Z�Ɠ_���v�Z�ɕ�������B �@��蕶�̓_���v�Z�Ƃ́A���m�_�Ԃ̌����ɂ�������W�l�̍��A����������ɂ��ē_��������̂ł���A1�`4���܂ł̊e�敪�ɂ����Ă��̋��e�l����߂��Ă���B��v�Z���l�ɁA���e�l���z������Ԃ͍đ��ƂȂ�B
�@�_���v�Z�̍H���͎��̂悤�ɂȂ�B �@ �W���̓_���v�Z �A ��ʏ�̋����y�тw�E�x���ʂɓ��e���ꂽ�����̌v�Z �B �ΐS��v�Z �C ���W�̓_���v�Z
�@����āA�� �� �� �� �� �� ���@�ƂȂ�A�͂S�ɂȂ�B
�F�S |
|
��No6�F��_���ʁF�� ��
���@��
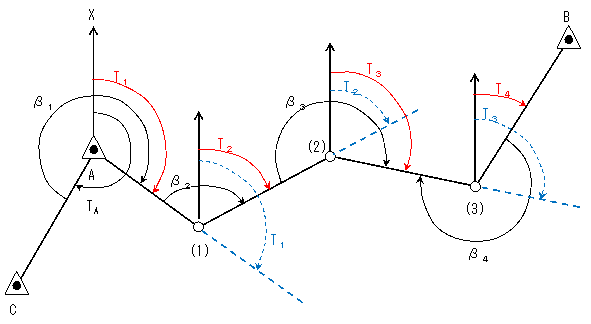
���}�̂悤�ɖ��̐}���ɕ⏕�������A���������p�����߂čs���Ηǂ��B
�}���A�V�_(�R)�ɂ�������m�_�a�ւ̕����p�i�s�S�j�����߂�ɂ́A�s�P���珇�Ԃɕ����p�����߂�悢�B
�E�`�_�ɂ�����(�P)�ւ̕����p �@�s�P���i�s�`�{���P�j�|360���� �i210��02��10���{ 275��59��31���j�| 360���� 126��01��41�� �E(�P)�_�ɂ�����(�Q)�ւ̕����p �@�s�Q���i�s�P�{���Q�j�|180���� �i126��01��41���{ 116��15��23���j�| 180���� 62��17��04�� �E(�Q)�_�ɂ�����i�R�j�ւ̕����p �s�R���i�s�Q�{���R�j�|180���� �i 62��17��04���{ 219��58��57���j�| 180���� 102��16��01�� �E(�R)�_�ɂ�����a�ւ̕����p �s�S ���o(360���|���S) �{ �s�R�p�| 180���� {(360���| 248��33��11��)�{ 102��16��01��}�|180�� �@�@�� 33��42��50��
����āA�V�_(�R)�ɂ�����A���m�_�a�̕����p�́A33��42��50���ƂȂ�B
�F�S |
|
��No7�F��_���ʁF�� (�]���藝) H6-2-A�EH9-2-C�EH20-2-D�i�o��@3�^16
�@��蕶�̐}�Ɏ��}�̂悤�ȕ⏕���������A����g���āA�ΐS��v�Z���s���悢�B
�@�}���AT�L�� 360���| {(360���|T)�|��2 �{��1} �ɂ���āA���߂��鎖������B�����ŁA�ΐS��ʂ�1�A��2�����ꂼ�ꋁ�߂�Ǝ��̂悤�ɂȂ�B
����1�̌v�Z�� �u���_�ԋ������ΐS�_�ɗאڂ���Ӂv�ł��邽�߁A�]���藝�ɂ�鎮��p���ĉ����B
�������ŁAsin96���Acos96����180���|96���� 84���Ƃ��āA���\�ɂ�肻�̒l�����߂�悢�B ���܂��A�����藝�ɂ��ΐS��v�Z�̌����ɒl�������Ă��A0.0633���Ƌ߂��l�ɂ͂Ȃ�B ����2�̌v�Z�� �u���_�ԋ������ΐS�_�ɑ��āA�Ό�����Ӂv�ł��邽�߁A�����藝�ɂ�鎮��p���ĉ����B �@ ����ʓI�ɂ́A�ρ��̒l��p���邪����͖�蕶���Ɏw������Ă��Ȃ��������߁A�i180��/�j��p�����B
�����ŁA�����藝���̂��̂�p���Ă����������o����B�����藝��p����ƁA���̂悤�ɂȂ�B
�������pT�L�̌v�Z�� �`���̎�����A�����pT�L�����߂�Ǝ��̂悤�ɂȂ�B T�L�� 360���| {�i360���|T�j�|��2 �{��1} �� 360���|�o�i360���|300���j�| 0.0337���{ 0.0636���p�� 360���|�@60.0299���� 299.9701�� �@�@��299��58��12.4��
����āA�ł��߂��I�����́A2�D��299��58��13���ƂȂ�B
�F�Q |
|
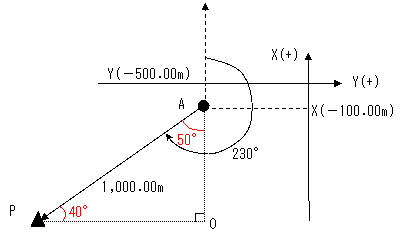
��No8�F��_���ʁF�� �@���W�v�Z�Ɋւ�����ł���B���ɑ��ʂ̒m����K�v�Ƃ�����̂ł͂Ȃ����A���W�������w���W�Ƌt�ł��邱�Ƃɒ��ӂ���K�v������B �@�܂��A��蕶��}�ɕ`���Ǝ��̂悤�ɂȂ�B
�}���_�o�̍��W�ʒu�����߂邽�߂ɂ́A�_�`����_�o�ɑ�������p��p���āA�C�ӓ_�n���܂߂��O�p�`�o�`�n�̓��p�����߁A�O�p����p���Čv�Z����悢�B
�@�܂��A�ڂo�`�n �� 230���|180���� 50�� �@���ɁA�O�p�`�o�`�n�ɂ�����A�ӂn�o�E�n�`�̒��������߂�ƁA �n�o��1,000�� �~ sin50���� 1,000�� �~ 0.7660 �� 766.04�� �n�`��1,000�� �~ cos50���� 1,000�� �~ 0.6428 �� 642.79�� ��sin�Ecos�̒l�́A�O�p���\�ɂ��B �������́A�����p���w�C�x���W���Ƀ}�C�i�X�����ł���B
�@���ɁA��蕶���̂`�_�̍��W�l�ɂ����������ƁA�o�_�̍��W�l�ɂȂ�B �w���W �� �|100.00 �� �{ �|642.79�� �� �|742.79�� �x���W �� �|500.00 �� �{ �|766.04�� �� �|1,266�D04��
����āA�_�o�̍��W�l�́A3�D�́i�|742.79�C�|1,266�D04�j�ƂȂ�B
�F�R |