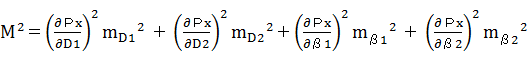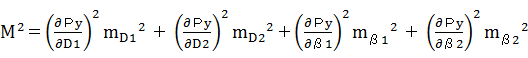| - PR - |
| - PR - |
|
��H27-No13�F�n�`���ʁF��
�@GNSS���ʋ@��p�����ו����ʂɊւ�����ł���B���e���ɂ��čl����Ǝ��̂悤�ɂȂ�B
�@����āC���炩�ɊԈ���Ă��镶�͂͂��C���ƂȂ�B
�F�@�R |
|
��H27-No14�F�n�`���ʁF��
�@�덷�`���Ɋւ�����ł���B�Δ�����p���Ď��̂悤�ɍl����Ηǂ��B
�@�`�`�b�̕����p�i��1�j�C�b�`�o�̕����p�i��2�j�����߂� �@��蕶�̊��m�_�`(205.000�C10.000)�C�a(20.000�C195.000)�̍��W�l���C
�@����āC��1����1�|180���|45������1�|225���C��2����1�{��2�|360���|45������1�{��2�|405��
�A�o�_�̂����W�Ƃ����W�����߂鎮��g���Ă� �`�b�Ԃ̋����F�c1�C�b�o�Ԃ̋����F�c2�@�Ƃ���ƁC �@�ox���`x�{�c1cos�i��1�|225���j�{�c2cos�i��1�{��2�|405���j �@�oy���`y�{�c1sin�i��1�|225���j�{�c2sin�i��1�{��2�|405���j�@�ƂȂ�B
�B�덷�`�d�̎����C�o�_�̂����W�̕W���������߂� �@ �@���C �@ �@ �@ �@�@ �@ �@�@ �@ �@ ����āC �@ �ƂȂ�B
�@�����ŁC�����̕������߂�ƁC
�@���ɁC�p�x�̕W�����͖�蕶���C
������C��L��A���ɑ������ƁC �@ �@ ����āC�l�� 22.8623�o �� 22.9�o�@�ƂȂ�B
�C �덷�`�d�̎����C�o�_�̂����W�̕W���������߂�
�@ �@���C �@ �@ �@ �@�@ �@ �@ ����āC �@ �ƂȂ�B
�@�����ŋ����̕��Ɗp�x�̕W������������ƁC �@ �@ ����āC�l�� 8.721�o ��8.7�o�@�ƂȂ�B
�F�@�o�_�̂w���W�̕W������ 22.9�o�C�x���W�̕W������ 8.7�o�@�@�ƂȂ�B |
|
��H27-No15�F�n�`���ʁF��
�@�C�����ʂɊւ�����ł���B���e���ɂ��čl����Ǝ��̂悤�ɂȂ�B �i�C�����ʁF�����̐��l�n�`�}�f�[�^�̃t�@�C�����X�V�����Ɓj
1.�������B1/500 �f�[�^�̓��x��1000�������ʂ������C�C���O�̃f�[�^�����쐬�N���V�������߁C�p���邱�Ƃ��ł���B
�F�@�Q |