| - PR - |
| - PR - |
|
��H26-No25�F���p���ʁi�H���j��
�@�N���\�C�h�Ȑ��̋Ȑ����y�ђP�Ȑ��̋Ȑ��������߁AP�`Q�Ԃ̘H���������߂���ł���B �@���̂悤�ɍl���ĉ����悢�B
�@�N���\�C�h�̊�{�������N���\�C�h�Ȑ��������߂�B �@R�EL��A�Q�@�@���AL��A�Q�^R ��80�Q�^100 �� 64��
�A�N���\�C�h�I�_�̐ڐ��p�i�сj�����߂�B �@�с� L�^ 2R �� 64�^(2�~100) ��0.32�~(180���^��) ��18��19��56��
�B�~�Ȑ��̒��S�p�����߂�B �@����I�|2�� �� 72���| 2�~18��19��56�� �� 35��20��08��
�C�P�Ȑ����̋Ȑ��������߂�B �@CL�� R�E�� �� 100�~35��20��08���� (180��/��) �� 61.680��
�@����āAP�`Q�Ԃ̘H�����͎��̂悤�ɂȂ�B 64.680���{64���{64����189.680����190��
�F�@�S
�����d��̎g�p���ł��Ȃ����߁A�A�̌v�Z��18��20���A�B�̌v�Z��36��40���Ƃ��Ă��ACL�̒l�́A100�~35��20����(180��/��)�� 61.676���ƂȂ�A�������ɓ�����e���͖����B |
|
��H26-No26�F���p���ʁi�p�n�j��
�@�p�n���ʂ̈�ʎ����Ɋւ�����ł���B�e�I�����ɂ��čl����Ǝ��̂悤�ɂȂ�B
1.�������B���}���̓]�ʂɂ����ē]�ʘA���}�́A�����Ȓ����͂����A���}���ɋL�ڂ���Ă���܂܂ɓ]�ʂ��쐬����B�i��ƋK���̏���
��396���j
�F�@�Q |
|
��H26-No27�F���p���ʁi�p�n�j��
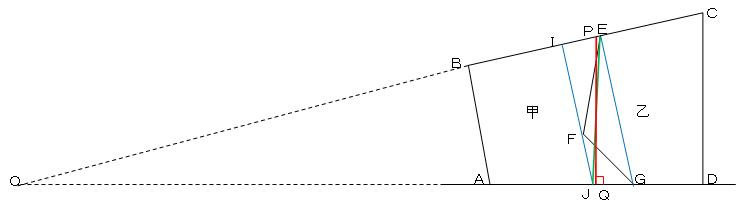
�@���E�����Ɋւ�����ł���B���̂悤�ɉ���悢�B
�@�e���W�l�����̂悤�ɍl����
�b�Ɖ��̖ʐς�ς����ɁA���E�̐������s���ɂ́A�����d�f�ƕ��s�œ_�e��ʂ���h�i�i�j�������A���̑Ίp�_�i�Ɠ_�d�����Ԑ��i�j�������悢�B�������A��蕶�ł͒����`�c�ɉ��낵�������o�p�i�ԁj�����E���Ƃ���Ƃ��邽�߁A���̂悤�ɍl����K�v������B
�����ŁA�b���̖ʐς�ς��Ȃ����߂ɂ́A���d�n�i�����o�n�p�ƂȂ�悢�����킩��B
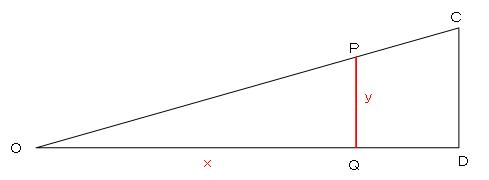
�B�i�_�̍��W�l�����߂� �@�i�_�̍��W�l�́A���v�Z�ɂ�莟�̂悤�ɋ��߂���B �@�_�d�Ɠ_�f�̈ړ��ʁ@�� ������36.50�|10.00��26.50�@�@�������|24.00�|�i�|23.50�j�� �|0.50 �@�_�e�Ɠ_�i�̈ړ��ʁ@�� ������ 0.00�i�����`�c��ɂ��邽�߁j �@�@�@�@�@�@�@�@�@�@�@�@ �����@26.5�F10��0.5�F���@���A����0.19 �@����āA�i�_�̍��W�l�́A����10.00�@�A���� �|36.00�|�i�|0.19�j���|35.81�@�ƂȂ�B
�C�n�_�̍��W�l�����߂� �@���a�b�̉�����ɂn�_�����邽�ߌ��z�͓���ł���B���a�b�̌��z�́A���W�l����10�F40�i�w��������10�s���ƁA�x��������40�i�ށj�ł��邽�߁A�n�_�̂����W�l���{10.00�ɂȂ邽�߂ɂ́A�b�_����|120.00�i�ꏊ�ł���ƍl������B ����āA�n�_�̍��W�l�́A����10.00�C�����|130.00 �ƂȂ�B �C���d�n�i�̖ʐς����߂�
�D�o�_�̂x���W�l�����߂�
�@�܂��A���}�̂悤�ɍl����B
�@�����ŁA�^����ꂽ���W�l���A�b�c�Ԃ�30.00�A�n�c�Ԃ�120.00�ł���B �܂��A���b�n�c�Ɓ��o�n�p�͑����`�ł��邩��A���̎������藧�B ����(30/120)����0.25���c(�`) ����ɁA�A�ŗ^�����悤�ɁA���d�n�i�����o�n�p �ƂȂ�悢���߁A0.5������ 1,248.02 �ƂȂ�A���̎���ϊ�����ƁA������ 2,496.04 �ƂȂ�B����ɁA�`���������āA�������߂鎟�̂悤�ɂȂ�B
0.25���Q�� 2,496.04�@�@�@����99.92
�@����āA�p�_�̂x���W�l�́A�n�_����{99.92�̈ʒu�ɂ��邽�߁A�|130.00�{99.92��30.08 �ƂȂ�A���Ƃ̍��W�l�ɖ߂��ƁA�|16,030.08 �ƂȂ�B
�F�@�Q |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
��H26-No28�F���p���ʁi�͐�j��
�@�͐쑪�ʂ̈�ʎ����Ɋւ�����ł���B���e���ɂ��čl����Ǝ��̂悤�ɂȂ�B
�F�@�P |