＜H26-No21：地図編集：解答＞

　地図の読図に関する問題である。問題各文について考えると次のようになる。

a.間違い。つつじヶ丘駅から女体山駅までの地図上の長さを測ると、約51�oである。問題文より、電子地形図25,000であるため、51�o×25,000 ≒ 1.3�q　となる。


※コンター：コンターライン（等高線）

b.正しい。つつじヶ丘駅の標高は約520ｍ、宮脇駅の標高は約300ｍである。

c.    間違い。直線部の最後の等高線（コンターライン）を読むと、標高520ｍである。



d.正しい。筑波山頂駅の標高が約780ｍ、宮脇駅の標高が約300ｍであり、その距離は1250ｍである。よって、（780ｍ−300ｍ）/1250ｍ＝0.384　 tanθ＝0.384 を関数表で引くと、約21°となる。



e.正しい。図上の図枠距離と標高点までの図上距離を測ると次図のようになる。



・経度の算出：図枠が2′で12�p、問題の標高点が図枠から2.9�pであるから、次の比例計算　
　により算出できる。
  2′：12�p ＝ ｙ：2.9�p　　　ｙ＝ 0.483′≒ 29″
  140°05′25″＋ 29″＝ 140°05′54″

・緯度の算出：図枠が1′で7.5�p、問題の標高点が図枠から6.6�pであるから、次の比例計
　算により算出できる。
　1′：7.5�p ＝ ｘ：6.6�p　　　ｘ＝ 0.88′≒ 53″
　36°12′40″＋ 53″＝ 36°13′33″
　よって、問題文は正しい。

f.正しい。高等学校「○で囲われた文」の地図記号はこの地図上に一つしかない。



g.間違い。水平距離 約2�q、斜距離 約2.1�q、高低差 約0.7�qとなる。

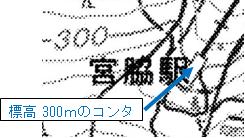
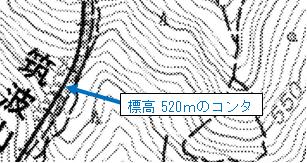
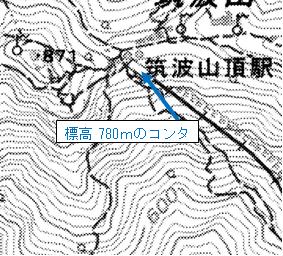
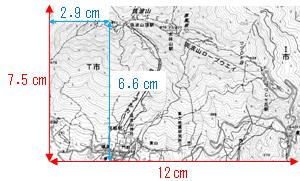
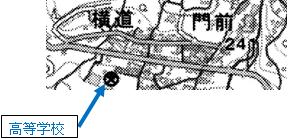
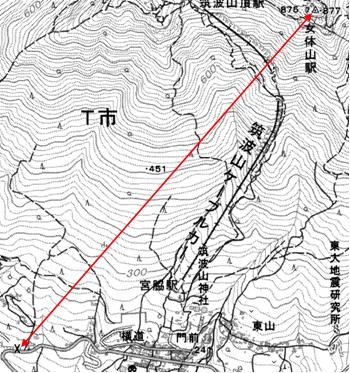
交番と女体山駅北側の三角点を直線で結んだ地図上の距離は7.9�p、電子地形図25,000であるため、0.079ｍ×25,000 ＝ 1.975�q ≒ 2�q、　　両点の標高を見ると、交番が約180ｍであるため、三角点との高低差は、877ｍ−180ｍ ＝ 697ｍ ≒ 0.7�q となる。水平距離2�qで高低差が0.7�qの斜距離を考えると、√(2^２＋0.7^２) ＝ √4.49 ＝ 2.1�q　となる。

　よって、明らかに間違っている文書は、ａ，ｃ，ｇ となる。

解答：　２

＜H26-No22：地図編集：解答＞

　ＵＴＭ座標系と平面直角座標系の特徴に関する問題である。正しい語句を当てはめると次のようになる。

a.UTM座標系及び平面直角座標系ともに、 ガウス・クリューゲル 図法を投影法として適用している。
b.UTM座標系及び平面直角座標系の座標軸の北は、ともに 真北 方向である。
c.UTM座標系では、中央経線から東西方向に約 180 km離れたところで、縮尺係数は1.0000となり、この距離を越えたところでは、縮尺係数が1.0000より 大きく なる。
d.UTM座標系の一つのゾーン（座標帯）における南半球の座標値は、原点より南、かつ、西に位置する地点の座標値はすべて 正（＋） である。
e.平面直角座標系の一つの系における座標値は、原点より南、かつ、西に位置する地点の座標 値はすべて 負（−） である。

　解答：　１

＜H26-No23：地図編集：解答＞

　地理情報標準(JSGI2.0)及びJMP2.0に関する問題である。問題各文について考えると次のようになる。

1.正しい。地理情報標準では、地理情報を異種システムにおいて相互利用する際に必要な、データ構造、記録方法、品質等を定めており、具体的なフォーマットを定めている訳ではない。

2.正しい。データを相互利用しやすくなり、異なる整備主体で整備されたデータの共用やシステムへの依存度が低くなるため、重複投資を排除する期待が持てる。

3.正しい。問題文の通り。共通のルールに沿って作成された製品仕様書は問題文のように使用する事ができる。

4.正しい。ISOにはコアメタデータを含む包括的メタデータ（約400項目）があり、JMP2.0ではこれと整合性を保ちながら、包括的メタデータから必要とされる項目をISOからピックアップしている。

5.間違い。位置情報は「住所」による記述である。

解答：　５

＜H26-No24：地図編集：解答＞

　地理空間情報活用推進基本法に関する問題である。問題各文について考えると次のようになる。

1.正しい。地理空間情報活用推進基本法 第2条3。

2.正しい。問題文のような基盤地図情報項目が含まれる測量成果を活用して整備・更新される。

3.正しい。地理空間情報活用推進基本法 第18条2。

4.間違い。基盤地図情報の項目としては、問題文にある項目を含み国土交通省令として13項目が定められている（測量の基準点、海岸線、道路区域界、河川区域界、行政区画の境界線、道路縁、河川堤防の表法肩の法線、軌道の中心線、標高点、水涯線、建築物の外周線、市町村の町若しくは字の境界線、街区の境界線）。この中に、問題文にある「道路の中心線」は含まれていない。

5.正しい。平面位置の誤差と高さの誤差がそれぞれ定められている。

解答：　４