| - PR - |
| - PR - |
|
�� H25-pm5-A�F�� ��
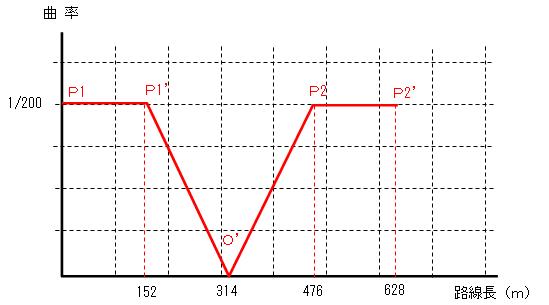
��A-1. �@�N���\�C�h�ڐ��p�i�сj�����߁A�ڑ�����~�Ȑ��̋Ȑ��������߂���ł���B �@���̂悤�Ɍv�Z����悢�B
�@�@�N���\�C�h�̊�{�������N���\�C�h�Ȑ��������߂�B �@�@R�EL��A�Q�@�@���AL��A�Q�^R ��180�Q�^200 �� 162��
�A�@�ڐ��p�i�сj�����W�A���ŋ��߂�B �@�@�с��iL�^2R�jrad�@���A162���^�i2�~200���j �� 0.405rad�@�@ �@��������p�x�ɒ����ƁA0.405rad �~�i180���^�j�� 23��12�f17�h�@�ƂȂ�B
�B�@�~�Ȑ��̋Ȑ��������߂�B �@�~�Ȑ��̒��S�p�i���j���h�| 2�т̂��߁A���� ��/2�i��90���j�| 2�~0.405 rad ��0.761rad �@�b�k�� 0.761rad �~200����152.159��
����āA�_�o1�ɂ�����ڐ��p�i�сj���@0.405rad �@�@�@�@�Ȑ��o1�`�o1'�̒����@��152���@�@�@�ƂȂ�B
��A-2. �@���H�c�f�}�ɂ���ȗ��}��`���悢�B������Ԃ͋ȗ����O�Ő������A�~�Ȑ���Ԃ͋ȗ������Ő������A�N���\�C�h��Ԃ͋ȗ������ő����i���ہj���鎖�������Ƃ��ĕ`���悢�B �@���̖��̏ꍇ�A�o1�`�o1�f��Ԃ�R=200���̉~�Ȑ��A�o1�f�`�o2��Ԃ̓N���\�C�h�̑g�����ŁA�n�f�͈�u�ȗ����O�ƂȂ�B ��A-3. �@�N���\�C�h�Ȑ��̓����Ɋւ�����ł���B a. �~�F�p�����x�@�@���p���x�ł͂Ȃ��A�p�����x�����ł���B�� b. �~�F�ȗ����a�@�@���ȗ����a���ő偁���̈ʒu�Őڑ�����遄 c. �F�������B
|
|
�� H25-pm5-B�F�� ��
��B-1. �H�����ʂ̍�ƍH���Ɛ��ʕi�Ɋւ�����ł���B
�A�F��BM�ݒu���ʁ@�@�F�ϑ����A���ʕ\�A�i���]���\ �C�F���S�����ʁ@ �@�@�F�v�Z��A���`�n�`�}�f�[�^�t�@�C���A���Ɠ_�} �E�F�p�n���Y�ݒu���� �F�v�Z��A�i���]���\
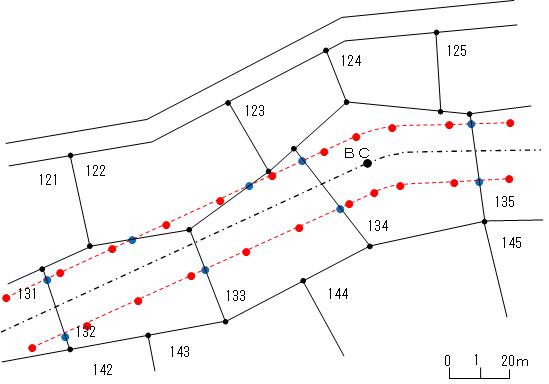
��B-2. �@��ƋK���̏��� ��350���i���`����@���@�@�_�����ʁj�Ɋւ�����ł���B �E�����_�Ԃ̋����𑪒肵�A���W�����狁�߂������Ƃ̔�r�ɂ��s���B
��B-3. �@��ƋK���̏��� ��361���@���f���ʂɂ�����_�����ʂ̕��@�ɂ��ċL�����ł���B �E�_�����ʗ��ɂ���đI�����ꂽ���f�ʂɂ��āA�ēx���f���ʂ����{���A���̌��ʂɊ�Â��ĕ`�悵�����f�ʐ}���A��ɕ`�悵�����f�ʐ}�̒��S�_�y�і��[���ʍY���Œ肵�ďd�ˍ��킹�A���f�`����r����B �E�_�����ʗ��ɂ���đI�����ꂽ���f�ʂɂ��āA���S�Y�Ɩ��[���ʍY�̋����y�ѕW���̑���l�Ɠ_�����ʒl�Ƃ̔�r���s���B |
|
�� H25-pm5-C�F�� �� �@ ��C-1. �@�������ʂ̒��ڕ����@�Ɋւ�����ł���B���̂悤�ɋL���Ηǂ��B
�E �c�����鋫�E�_�y�іS���������E�_�̐��ʂɊ�Â��A���ʖ@�ɂ�蕜������B �E �c�����鋫�E�_�y�іS���������E�_�̐��ʂɊ�Â��A���˖@�ɂ�蕜������B �E ���Ɠ_���g�p���A�Q��̃Z�I�h���C�g��p���āA���̎������̌�_�Ƃ���B
��C-2. ��C-3. �@��ƋK���̏��� ��4408���@���E�_�ԑ��ʂɊւ�����ł���B �E�g�[�^���X�e�[�V�����̑Εӑ���@�\��p���ċ��E�_�ԋ����𑪒肵�A�v�Z�l�Ƃ̊r���ɂ�萸�x���m�F����B �E���E�_�̍��W����ɗp�������m�_�ȊO�̊��m�_���狁�߂����W�l�Ɋ�Â����E�_�ԋ����Ƃ̊r���Ő��x���m�F����B |
|
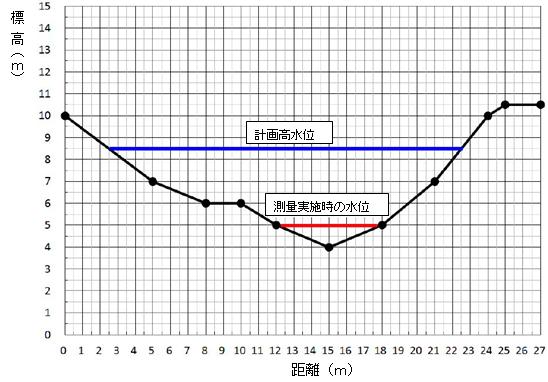
�� H25-pm5-D�F�� ��
��D-1. ��D-2.
��D-3.
�A�F���ʐ���i���ʂ�����j�@�@�C�F���ۍY�@�@�E�F�H�����ʁ@�@�G�F���ʁi���͒��ʁj |