＜ H25-pm4-A：解答例 ＞

　平面直角座標系に関する問題。

1.    ○
2.    ×　　中央計算から離れるほど長く投影される。
3.    ×　　東西90km以内のすべての地点は縮尺係数が1.0000以下となる。
　　（東西90�q以上のすべての地点は、縮尺係数が1.0000以上となる。）
4.    ×　　北半球では、N=0km、E=500km、南半球では、N=10,000km、E=500km としている。
5.    ○

＜ H25-pm4-B：解答例 ＞

問B-1.

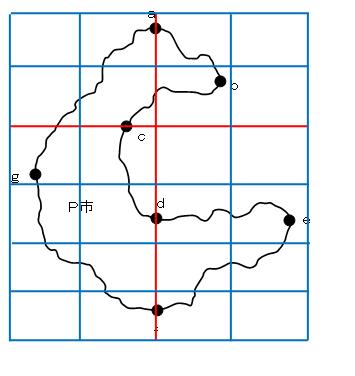
　図葉の区画割りを考える問題である。次のように考えれば良い。

�@    1/5,000 地形図で、縦60�p、横80�pの図郭であるため、１枚の地形図がカバーする図郭のエリアは、縦3,000ｍ、横4,000ｍとなる。

�A    平面直角座標系の原点を基準とした図郭線であるため、点ａ、ｄ、ｆが図郭線上に乗る事になる。また、同様に点ｃも図郭線上にあるため、この２本の線（赤線）を基準に考えて行けばよい。

これらを基に図を描くと、次のようになる。

　よって、必要な図葉数は、１７枚となる。

問B-2.

　管内図の最大縮尺を求める問題である。次のように考えれば良い。

　ａ、ｆ点のＸ座標値の差は、26,500−11,000＝15,500ｍ　である。これを縦100�pの図郭内に描く事を考えると、1/15,500 となる。

　また、ｅ、ｇのＹ座標値の差は、11,400−（−2,400）＝ 13,800　である。これを横70�pの図郭内に描く事を考えると、0.7/13,800 ＝ 1/19,714　となる。

　問題文より、縮尺分母数は1,000の倍数であるため、Ｐ市の全域が１枚の図葉に収まるための最大縮尺は、1/20,000　となる。

＜ H25-pm4-C：解答例 ＞

問C-1.

　JPM2.0（メタデータ）に関する問題である。ア〜オには次の語句が入る。

ア ：重複投資

イ ：クリアリングハウス

ウ ：識別情報

エ ：参照系情報

オ ：保守情報

問C-2.

　データ品質要素に関する問題である。ア〜オには、次の語句が入る。

ア ：位置正確度

イ ：完全性

ウ ：主題正確度

エ ：論理一貫性

オ ：時間正確度

＜ H25-pm4-D：解答例 ＞

　問D-1.

　Ａ、Ｂ間の出力図上距離と座標距離を求めてから出力図の縮尺を求め、縮小率を計算すればよい。

�@Ａ、Ｂ間の出力図上の距離（ｓ）を計算すると次のようになる。
�凾�＝ 12.1− 108.1 ＝ −96.0�o

　�凾凵� 63.4− 32.2  ＝ 　31.2�o

�AＡ、Ｂ間の座標間距離（Ｓ）を�@と同様に計算すると次のようになる。

　�凾w＝ −947.740 −（−1066.400）＝ 118.660 ｍ

　�凾x＝ 3730.010 − 3566.680 ＝ 163.330 ｍ

�B出力図の縮尺を求めて縮小率を考えると次のようになる。

　（出力図の縮尺分母）＝ 201.883ｍ ÷ 100.943�o ＝ 1999.974 ≒ 2000

よって、1/10,000 の地形図上に定位する場合の縮尺率は、

　10,000 ÷ 2,000 ＝ 5　　　よって、縮小率は 1/5 となる。

問D-2.

　出力図のｙ軸の平面直角座標系に対する回転角を求める問題である。次の手順で解答すればよい。

�@出力図上のｙ軸からＡＢへの方向角（α1）を求めると次のようになる。

※ｘ，ｙの値を逆に計算するため、�凾�＝−31.2、�凾凵�96.0とする。

　よって、α1＝180°− 71°59′45″＝ 108°00′15″

※ｘ＝−、ｙ＝＋の符号であるため、方向角は、180°−θ となる。

�A座標上のＡＢへの方位角（α2）を求めると次のようになる。

　　よって、α2＝54°00′05″

※Ｘ＝＋、Ｙ＝＋の符号であるため、方向角は、θ＝α となる。

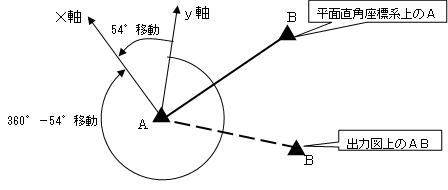
�B回転角については、次図のように考えると良い。



よって、回転角は 360°−54°＝ 306°　となる。