| H25年度 測量士試験 午前 No9~No12 水準測量 |
|
|
<H25-No9:水準測量:解答>
水準測量の観測作業の注意事項に関する問題である。問題各文について考えると次のようになる。
a.
間違い。
鉛直軸誤差の累積を防ぐために、レベルの三脚は進行方向に対して左右交互に整置するのが正しい。また、レベルの整置は望遠鏡を常に同一の方向に(特定の標尺に)向けて行う必要がある。
b.
間違い。
楕円補正量は、観測点の緯度と標高により求める。正規標高補正量とは、各水準点における重量値を用いて、水準測量による高低差を厳密な高低差に変換する値(式)である。通常の公共測量では、楕円補正が用いられる。楕円補正量は緯度に関係するが、経度には無関係である。
c.
正しい。
標尺補正量(⊿C)は、⊿C={C0+(T-T0)α}⊿H の式で与えられる。標尺定数(改正数):C0 、膨張係数:α
、気温:T0 ,T 、高低差:⊿H となる。
d.
正しい。
作業規程の準則 第63条2 1・2級水準測量においては観測作業中おおむね10日ごとについても行う。
e.
正しい。
両岸からの同時観測は、経緯儀法、俯仰ねじ法で用いられる。どちらの方法でも観測距離が長くなるため、大気密度の変化による影響が大きいため、同時観測を行うなど、影響を最小にする必要がある。
よって、明らかに間違っているのは、aとbである。
解答: 1
|
|
|
|
<H25-No10:水準測量:解答>
水準測量の点検計算における、再測路線の判断に関する問題である。単位水準環(閉路線)ごとに点検計算を行えばよい。
|
No
|
単位水準環
|
閉合差
|
閉合差の許容値
|
合否
|
|
1
|
A → B →
C
|
+2.3080+1.2670-3.5910=
-0.0160m
|
5㎜√(3+2+4) =0.0150m
|
OUT
|
|
2
|
B → C →
D
|
+1.2670+1.6050-2.8800=
-0.0080m
|
5㎜√(2+2+5) =0.0150m
|
OK
|
|
3
|
A → C →
D
|
+3.5910+1.6050-5.1730=
+0.0230m
|
5㎜√(4+2+10) =0.0200m
|
OUT
|
|
4
|
A → B →
D
|
+2.3080+2.8800-5.1730=
0.0150m
|
5㎜√(3+5+10) =0.0212m
|
OK
|
よって、許容値を超えている2つの水準環に共通する路線
A→Cを再測すればよい。
解答: 2
|
|
|
<H25-No11:水準測量:解答>
水準測量における観測方程式に関する問題である。ア~オに入る語句を考えると次のようになる。
ア:0.0040
式11-1において、新点Cの仮定標高は3.3500m であるため、
3.3500-(10.2000-5.2020-6.8540)=5.2060
5.2060-5.2020=0.0040
もしくは、3.3500-(5.0000+5.2020-6.8540)+0.0020=0.0040
イ:-1
V1-V2=2XB-1XC-0.0060=0 となる。
ウ:+0.0045
V3の路線長が2㎞であるため、方程式の重量を1/2とすると、
V2+V3/2=-XB+1.5XC+0.0045=0 となる。
エ:10.2023
正規法的式を解くと、XB=+0.0023 XC=-0.0060となる。
よって、10.200+0.0023=10.2023 となる。
オ:3.3485
エと同様に、3.3500-0.000015=3.3485となる。
解答: 1
|
|
|
<H25-No12:水準測量:解答>
水準測量の往復差による1㎞当たりの標準偏差を求める問題である。次のように解答すればよい。
|
路線
|
S
|
δ
|
δδ
|
(δδ)/S
|
|
A → B
|
2.0㎞
|
0.8
|
0.64
|
0.320
|
|
B → C
|
1.5㎞
|
1.2
|
1.44
|
0.960
|
|
C → D
|
1.6㎞
|
2.0
|
4.00
|
2.500
|
|
D → E
|
2.0㎞
|
2.3
|
5.29
|
2.645
|
|
合計
|
|
|
|
6.425
|
①1㎞当たり(重量1)の、片道の標準偏差(m0)を考える。
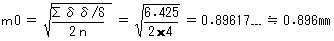
②往復の標準偏差(m)を考える(誤差の伝搬)
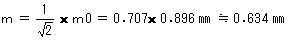
よって1㎞当たりの標準偏差は、0.64 ㎜ となる。
解答: 2
※前式を公式化して、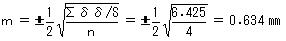 としても求められる。 としても求められる。
|
|
| 参考文献:公共測量作業規程の準則・測量法 |
|
(c) Sey Quo De La Jarantos & (c) Matsubara.P.O 2013 |