| - PR - |
| - PR - |
|
��H25-No5�F��_���ʁF��
�@�g�[�^���X�e�[�V�����i�ȉ� �s�r�j�ɂ�鋗������i���g�����V�j�Ɋւ���덷�̖��ł���B��蕶�ɍł��K���Ȍ��Ă͂߂�Ǝ��̂悤�ɂȂ�B
�A�F��C�̋��ܗ� �C�F�オ�� �E�F�Z���Ȃ� �G�F�Ⴍ�Ȃ� �I�F�Z���Ȃ�
����āA���������̑g�����́A�T �ƂȂ�B
�F�@�T
�s�r�̋����ɔ�Ⴗ��덷�ɂ́A�u�C�ہi�C���E�C���E���x�j�v�Ɓu�ϒ����g���v������B�܂��A��Ⴕ�Ȃ��덷�ɂ́A�u��B��v���Y���萔�v�A�u�ʑ�������v�A�u�v�S�v�ɂ����̂�����B
�s�r�ɂ�鋗������ł́A�u��ƋK���̏����i�t�U�j�v�Z���W�v �ɋC�ە�������邪�A�ȗ��������ߎ����ł́A�C���A�C���A���x�̂��ꂼ��̕ω��ʂ��A��t�i���j�A��P�ihPa�j�A��e�ihPa�j�Ƃ���ƁA�@��D���i�{1.0��t �| 0.3��P �{ 0.04��e�j�~ D �~ 10�|�U�@�ƕ\�����B �@ �@���̋ߎ����ɁA��蕶�Ă͂ߍl����ƁA�Ⴆ�A�ϑ����̋C������t�����オ��ƁA ��D�� �{1.0�~�i�{��t�j�~ D �~ 10�|�U �ƂȂ�A��D �� 0 �i�{��D�j�ƂȂ邽�߁A���蒷 D�r �͎��ۂ̋������Z���Ȃ鎖���킩��B�܂�AD�i���ۂ̋����j �� D�r�i���苗���j �{ ��D�i�C�ە�ʁj�ł��邽�߁AD�r �� D �| ��D �ƂȂ�A���苗���͎��ۂ̋������A�Z���Ȃ鎖���킩��B
�@���l�ɋC������P�����Ⴍ�Ȃ�ƁA��D�� �|0.3�~�i�|��P�j�~ D �~ 10�|�U �ƂȂ�A��D �� 0 �i�{��D�j�ƂȂ邽�߁A���蒷 D�r �͎��ۂ̋������Z���Ȃ鎖���킩��B |
|
��H25-No6�F��_���ʁF��
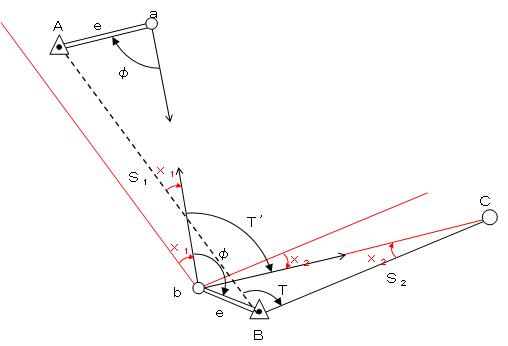
�@�ΐS��v�Z�Ɋւ�����ł���B�}�̂悤�ɁA��蕶�ɕ⏕����������Ɖ��Ղ��B �O�}�ɂ����āA��1���`�a�̕ΐS��ʁA��2���`�b�̕ΐS��ʂƂ���ƁA�ڂ`�a�b�͎��̂悤�ɕ\�������ł���B
�@�ڂ`�a�b �� �s���{ ��1 �| ��2�@
�@�����ŁA��1�A��2�Ƃ��ɁA������Ꭾ�ŋ��߂鎖���ł��邽�߁A���̂悤�Ɍv�Z���鎖���ł���B
�i�`�a�̕�ʁj
sin��1 �� �i��1�~sin ��1 �{��2�~sin��2�j�^ �r1 �� �i2.00�~sin90���{1.00�~sin150���j�^1200
sin��1 �� 1/480 �@����āA��1 ���i1/480�j�~�ρ� �� 416.667 �� ���@0��06��57��
�i�`�b�̕�ʁj
sin��2 ���i��2�^1000�j�~sin(��2�|�s��) �� �i1.00�^1000�j�~ sin�i150���|90���j
����āA��2 ���i0.001�~ sin60���j�~ �ρ��� 173.205���� 0��02��53��
����āA�ڂ`�a�b �� 90���{ 0��06��57���| 0��02��53���� 90��04��04���@�ƂȂ�B
�F�@�S |
|
��H24-No7�F��_���ʁF��
�@GNSS�Ɋւ����b�I�Ȗ��ł���B���������Ă͂߂�ƁA���̂悤�ɂȂ�B
�A�F���V���q�� �C�FGLONASS �E�F������^GPS�q�� �G�F�d�q��_
�@���{���ł��グ�Ă���̂́A���V���q���i�݂��т��j�ł���A���V�A��GLONASS�i�O���i�X�j�AEU��Galileo�i�K�����I�j�ł���B�������܂�GPS�q���̃u���b�N�V�V���[�Y�ȂǁA������^GPS�V�X�e���̊g�[���}����\��ł���A����ɑΉ����邽�ߓd�q��_�������Ή��ł���悤������������Ă���B
�F�@�R |
|
��H25-No8�F��_���ʁF��
�@GNSS���ʂ̓����ɂ��ďq�ׂ����̂ł���B���e���ɂ��čl����Ǝ��̂悤�ɂȂ�B
�F�@�T |