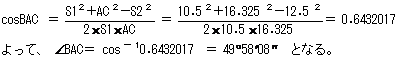| - PR - |
| - PR - |
|
��H25-No25�F���p���ʁi�H���j��
�@�N���\�C�h�Ȑ��̋Ȑ��������߁A�N�_�iNo0�j����N���\�C�h�I�_�iKE�j�܂ł̘H���������߂���ł���B���̂悤�ɍl���ĉ����悢�B
�@�N���\�C�h�̊�{�������N���\�C�h�Ȑ��������߂�B �@R�EL��A�Q�@�@���AL��A�Q�^R ��180�Q�^200 �� 162��
�A�N�_����N���\�C�h�I�_�܂ł̘H���������߂�B �@��蕶���A�N�_����N���\�C�h�n�_�iKA�j�܂ł̘H������60���ł��邽�߁A 60���{162����222�� �@����āA�N�_����KE�܂ł̘H�����́A222���@�ƂȂ�B
�@�F�@�T
����蕶�̌��� �@�{��ɂ����ĕ����̐��l�����̂܂ܗp����ƁA��ӂ̂悤�ȋȐ��ݒu���s�����͂ł��Ȃ��Ȃ�B
�@��̓I�Ɍ���ƁA�~�Ȑ��̒��S�p�i���j��I�|2�с@�@�i�����ŁA�с�L�^2R �E180���^�j �@�̎��ɖ�蕶�̐��l�������Ă݂�Ǝ��̂悤�ɂȂ�B
�@�с� �i162���~180���j�^�i2�~200���j�@�� 29160�^1256 ��23��13��00�� �@����45���| �i2�~23��13��00���j�� �|1��26��00���i358��34��00���j �@�܂�~�Ȑ��̕����������Ȃ�ǂ��납�A�N���\�C�h�Ȑ��ǂ������d�����镔�����ł��Ă��܂��B �@�ɉe���������Ƃ͌����A���������������̂�����쐬���K�v�ł͂Ȃ����H |
|
��H25-No26�F���p���ʁi�p�n�j�F��
�@�p�n���ʂ̈�ʎ����Ɋւ�����ł���B�e�I�����ɂ��čl����Ǝ��̂悤�ɂȂ�B
�F�@�T |
|
��H25-No27�F���p���ʁi�p�n�j�F��
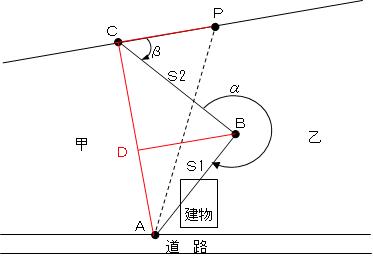
�@�y�n���E���̐����Ɋւ�����ł���B���̂悤�ɁA�⏕���������čl����Ηǂ��B
�@�]���藝�i��Ӌ��p�j�ɂ��A��BAC�����߂�B �@�܂��A��AC�̒��������߂�ƁA
�@��BAC�̑傫���́A
�A�a�_�����AC�ɂ����鐂���̒����iBD�j���l����B �@BD �� AB�~sin BAC �� 10.5�~sin49��58��08�� �� 8.040���@�ƂȂ�B
�B��APC�̑傫�������߂�B �@��ACP�� 180���|�i49��58��08���{�i360���|270���j�j�{45���� 85��01��52�� �@ �CCP�Ԃ̋��������߂�B �@��ӂ��A�b���Ԃ̖ʐς�ς����ɋ��E���̐������s���ɂ́A�O�p�`ABC�ƎO�p�`APC�̖ʐς��ɂ���悢�B����āA�O�p�`APC�̍�����8.040���ƂȂ�悤�ɁA��CP�̒��������肷��悢���ɂȂ�B �@����āA �@
�F�@�R |
|
��H25-No28�F���p���ʁi�͐�j�F��
�@�͐쑪�ʂ̈�ʎ����Ɋւ�����ł���B�e��蕶�ɂ��čl����Ǝ��̂悤�ɂȂ�B
�@����ĊԈ���Ă����蕶�́A���A�� �ƂȂ�B
�F�@�S |