<H24-pm2-A：解答>

　作業規程の準則 第24条（及び関連）に関する出題である。

　ア〜コに入る語句を考えると次のようになる。

ア：作業計画 （第11条）

イ：選点（第30条）

ウ：現況調査（第27条）

エ：点の記（第33条）

オ：観測値（第37条）

カ：点検測量（第38条）

キ：精度管理表（第42条）

ク：製品仕様書（第44条）

ケ：成果等の整理（第15条）

コ：メタデータ（第45条）

<H24-pm2-B：解答例>

問B-1.

　観測セッションの組成に関する問題である。各セッションにおける新点数を考慮すると、次図のようになる。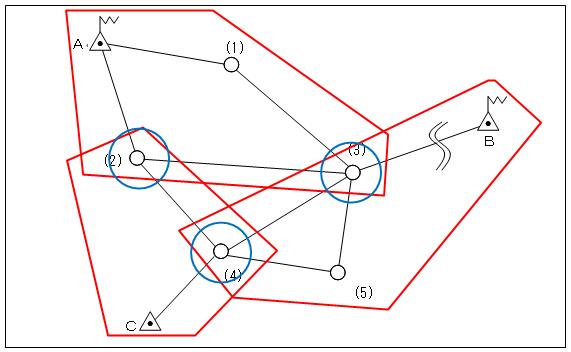

　問題文に、「GNSS測量機を３台」とあるので（既知点数も３）、セッションは３つとなる。また、(2)、(3)、(4)の新点が、各セッションに重複するように囲めば良い。これにより、(2)〜(3)〜(4)が基線となる。

　問題文より、既知点Ａ，Ｂが電子基準点、既知点Ｃが三角点である事を考えると、新点の数をＡ，Ｂに多く、Ｃに少なくすれば良い。　

　3つ目のセッションはC〜(2)〜(3)〜(4)とも考えられるが、問題文に「最も効率的な観測」とあるため、解答のセッションが最良と考えられる。

問B-2.

　B-1の解答より、　(2)〜(3)〜(4)　となる。

問B-3.

　既知点を電子基準点のみとしない場合、

「仮定三次元網平均による、許容値から既知点成果の良否を判断。」

　※既知点成果の問題の有無を検証すればよい。既知点成果に問題があれば、未知点扱いにして別の既知点を用いる必要がある（新点数が５点であるため）。

　※電子基準点のみの観測の場合は、「仮定…」は不要である。

<H24-pm2-C：解答例>

問C-1.C-2 ともに、作業規程の準則 第23条2 からの出題である。

問C-1.

・１個の多角網における既知点数

・単位多角形の辺数

・路線の辺数

・節点間の距離

・偏心距離の制限

・路線図形

　など…。

問C-2.

「１個の多角網における既知点数」

1個の多角網における既知点数は、2＋新点数／5 以上で、端数を切り上げる。

「単位多角形の辺数」

10辺以下

「路線の辺数」

5辺以下。ただし、伐採樹木及び地形の状況等によっては､計画機関の承認を得て辺数を増やすことができる。

「節点間の距離」

250ｍ以上

「偏心距離の制限」

節点間距離／偏心距離 が６以上であること。

「路線図形」

多角網の外周路線に属する新点は､外周路線に属する隣接既知点を結ぶ直線から外側40 ﾟ以下の地域内に選点するものとし、路線の中の夾角は､60 ﾟ以上とする｡

など…。

<H24-pm2-D：解答例>

問D-1.

・(1)〜(2)〜(3)の環閉合の閉合差は、

＋10.1414＋5.5921−15.7395 ＝ −0.0060　　よって、−6.0�o　となる。（＋6.0�oでも良い）

・許容範囲は問題文より、2.0�o√S　であるため、

　S=60km+40km+25km=125km　2.0mm√S ＝ 22.3606…　　よって、22.3�o となる。

問D-2.

　再測すべき路線は、(5) となる。

※(6)→(3)←(5)　の閉合差は、−0.0246ｍ ＝ −24.6�o　よって、許容値（21.4�o）をオーバーしている。

※(4)→(5)←(2)　の閉合差は、＋0.0346ｍ ＝ ＋34.6�o　よって、許容値（22.8�o）をオーバーしている。

　理由

　(1)→(2)←(3)のみが許容値を満足している。また、(6)→(1)→(4)の閉合差も、4�o ＜ 26.8�oと許容値内にある。つまり、(1)〜(4)、(6)の観測結果は良好であると言える。よって、残った(5)の路線を再測すべきと言える。

問D-3.

　・往復観測差の大きい水準点間を再測する。

　・閉合条件を持たせ許容値を超えた水準点間を再測する。

　など

※問題文に「効率よく」、「適切に選択」とあるため、上記の２点に絞られると考える。