| - PR - |
| - PR - |
|
<H20-7-A�F��>
�@�N���\�C�h�Ȑ��̐ݒu�Ɋւ����{�I�Ȗ��ł���B�N���\�C�h�Ɋւ����{�I�Ȍ�������������Ɨ������Ă����K�v������B���̂悤�ɍl����悢�B
������68.5���̏ꍇ��
�F�R ������75.678���̏ꍇ��
�F�Q |
|
<H20-7-B�F��>
�@�H�����ʂ̍�ƍH���Ɋւ�����ł���B�m��x���̏o��ł��邽�߁A���̒��x�͊m���ɂł���悤�ɂ������B �@��蕶�ɂ���e�H�������ɕ��ׂ�Ǝ��̂悤�ɂȂ�B
a�D ���`����@�@���@e.���S�����ʁ@���@c.��BM�ݒu���ʁ@���@b.�c���f���ʁ@���@d�D�ڍב����@���@d.�@�p�n���Y�ݒu����
�@����āA�Q�̑I�����������ƂȂ�B
�F�Q
���@���y��ʏȔ������Ƃł͗p�n���Y�ݒu���p�n���ʂłȂ��H�����ʂɑg�ݍ��܂�ĐώZ����邱�Ƃ�����B |
|
<H20-7-C�F��>
�@�y�n�̕����Ɋւ�����ł���B�菇��ǂ��ĉ����čs���ΕK����������ł���B �@���̂悤�ɍl���čs���悢�B
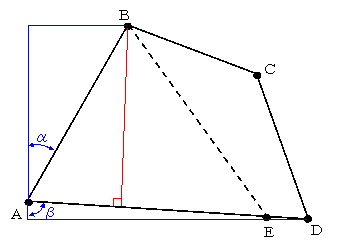
�P�D�l�p�`�`�a�b�c�̖ʐς����߂�B
�@�@�O�p�`�`�a�d�̖ʐς��`�a�b�c�� 2/3 �ɂ���Ηǂ����߁A1632 �� 1.5 �� 1088 �u �E�ڃ��@�F�@32��39��39�� �E�ڃ��@�F�@81��01��38�� ������A��A �� 66��18��48��
�` �� �d�ɗ��Ă��a�̐����́A�@
����āA�` �� �d�̒����́A1088 �� 42.422 �~ 2 �� 51.294 �� 51.3m �ƂȂ�B
�F�S |
|
<H20-7-D�F��>
�@�͐쑪�ʂɊւ����b�I�Ȗ��ł���B�m��x���̖��ł��邽�߁A���̒��x�͂�������Ɨ������Ă��������B���e���ɂ��čl����Ǝ��̂悤�ɂȂ�B �F�R |