|
<H18-5-A�F��>
�@�ʐ^�Ɏʂ����܂ꂽ�����Ԃ̕��ϑ��x���A�^����ꂽ��������苁�߂���ł���B��@�Ƃ��Ă͈ȉ��̂悤�ɁA�^����ꂽ���������k�ڂ𐄒肵�A�Βn���x�����肷�邱�Ƃɂ�蕽�ϑ��x�����߂�Ɨǂ��B
1.�����Ԃd�̈ړ����x����ړ����������߂�B
��蕶���A�����Ԃd�̕��ώ�����36km/h�A�Q���̎ʐ^�̎B�e�Ԋu��23�b�ł��邽�߁A
�i36,000m�~23�b�j�^3,600�b �� 230m
2.�K���Ȏʐ^�k�ڂ����肵�A�����Ԃd�̈ړ������i230m�j�ɂ��Ȃ����m�F����B
���̂悤�Ȗ��̏ꍇ�́A�������Ɣ䍂�̊W��
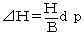 �@ �@
�i���g�F�䍂�A�g�F�Βn���x�A�a�F�B�e������A�����F�������j
���A�����Ԃ̈ړ����������߂邱�ƂɂȂ�B
�����ŁA���Ɏʐ^�k�ڂ��^�����Ă��Ȃ����߁A���L�̗l�ɂ�������肵�Βn���x�ƎB�e�����������1.�Ōv�Z���������Ԃ̈ړ������ƍ��v���邩�ۂ��m�F���A�����Ԃe�̈ړ����������߂�悢�B
�����ŁA��ʓI�ȋʐ^�̏k�ڂł���A1/10,000��1/12,500�ɂ��Č�������Ǝ��̂悤�ɂȂ�B
�E1/10,000�̏ꍇ�A�Βn���x�́A0.15m�~10,0000 �� 1,500m�A����āA�����Ԃd�̈ړ������́A
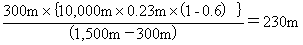 �@ �@
�ƂȂ�A1.�̈ړ������ƈ�v����B
�E1/12,500�̏ꍇ�A�Βn���x�́A0.15m�~12,5000 �� 1,875m�A����āA�����Ԃd�̈ړ������́A
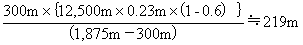 �@ �@
�ƂȂ�A1.�̈ړ������ƈ�v���Ȃ��B
����āA���̊ϑ��͑Βn���x1,500m�̊ϑ��ł���Ɛ����ł��A�����Ԃe�̈ړ������́A�ȉ��̂悤�Ɍv�Z�ł���B
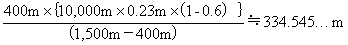 �@ �@
3.�����Ԃe�̑��x�����߂�B
�i334.545�cm �~ 3600�b�j�^ 23�b �� 52,363.636�cm/h �� 52km/h
�F�@�S
|