| - PR - |
| <R06-No5:法規・条約:解答> 正規分布表の読み方(見かた)に関する問題である。 問題文は、測定値がある数値内に入る確率を問うているため、正規分布表からzの値を求め、次のように考えればよい。 ※正規分布表:平均0で標準偏差が1のグラフ。ある範囲にどのぐらいのデータが含まれているのかを知ることができる。 正規分布表の確率は、z値(μ値)によって、次の式により求めることができる。 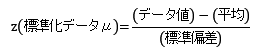 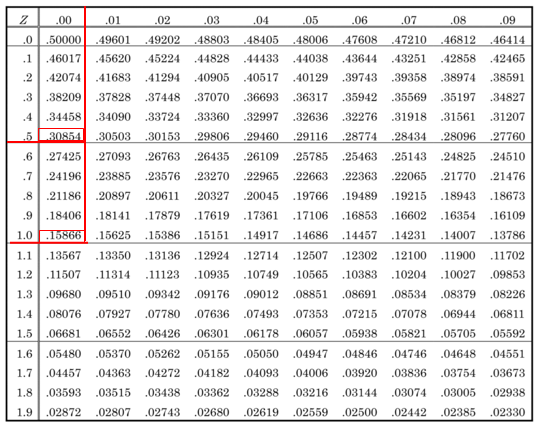 まず、zの値を求めると次のようになる。 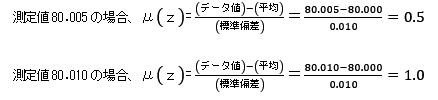 これから、正規分布表の確率を求めると、0.30854と0.15866となる。 よって、測定値80.005〜80.010の間になる確率は、 0.30854−0.15866=0.14988≒0.15 よって、この測定値の間になる確率は1.の15%となる。 |
| 解答: 1 |