| - PR - |
| پƒR02-No27پF‰—p‘ھ—تپi—p’nپjپF‰ً“ڑپ„ پ@‹«ٹEگ®گ³‚ةٹض‚·‚éŒvژZ–â‘è‚إ‚ ‚éپBژں‚ج‚و‚¤‚ة—]Œ·’è—‚ئچہ•W–@‚ة‚و‚é‰ً–@‚ھ‚ ‚éپB پƒ—]Œ·’è—‚إ‹پ‚ك‚é•û–@پ„ 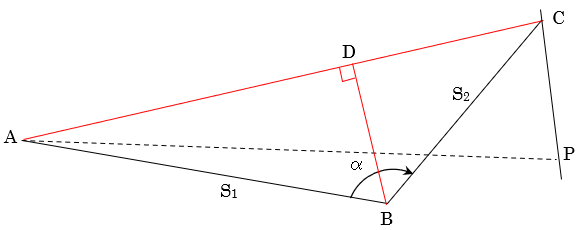 ‡@پ@گ}‚ة‘Oگ}‚ج‚و‚¤‚ب•âڈ•گü‚ً“ü‚ê‚ؤچl‚¦‚éپB ‡Aپ@•سAC‚ج’·‚³‚ً‹پ‚ك‚éپB 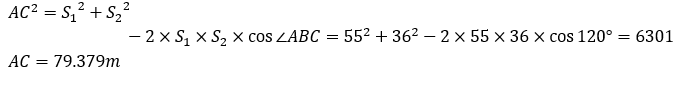 ‡Bپ@پعBAC‚ج‘ه‚«‚³‚ً‹پ‚ك‚éپB 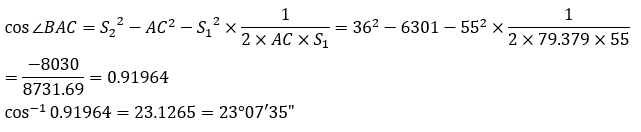 ‡Cپ@BD‚ج’·‚³‚ً‹پ‚ك‚éپB ‡Dپ@پعACP‚ً‹پ‚ك‚éپB ‡ECPٹش‚ج‹——£‚ً‹پ‚ك‚éپB ‡™ABC‚ئ‡™APC‚ج–تگد‚ً“¯‚¶‚ة‚·‚ê‚خ‚و‚¢‚½‚ك 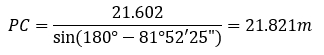 ‚ئ‚ب‚éپB پƒچہ•W–@‚إ‹پ‚ك‚é•û–@پ„ پ@گ}‚و‚èپACP‚ًXژ²‚ئ‚·‚é‚ئژںگ}‚ج‚و‚¤‚ة‚ب‚éپB 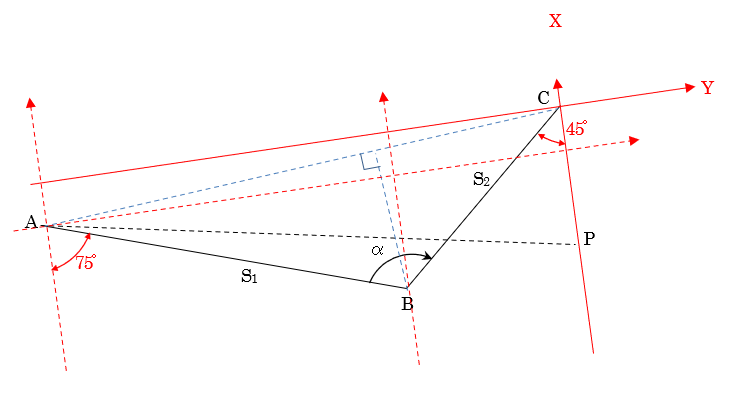 ‡@پ@•سAC‚ج’·‚³‚ً‹پ‚ك‚éپB 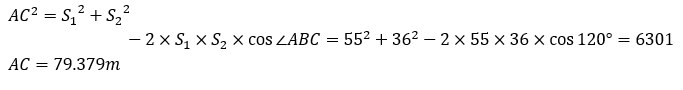 ‡Aپ@ٹe“_‚جچہ•W’l‚ً‹پ‚ك‚éپB C“_‚ًŒ´“_پi0پC0پjپAP“_‚ًپixپA0پj‚ئ‚·‚é‚ئپA  ‡Bپ@‡™ABC‚ج–تگد‚ً‹پ‚ك‚éپB 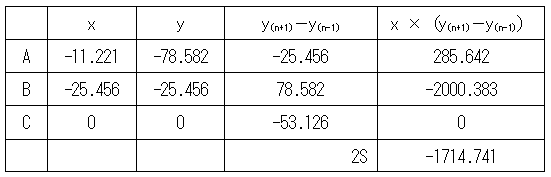 ‡Cپ@‡™ACP‚ج–تگد‚ً‹پ‚ك‚éپB 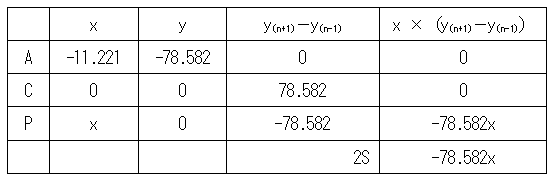 ‡Dپ@P“_‚ج‚کچہ•W‚ً‹پ‚ك‚éپB ‡™ABC‚ئ‡™ACP‚ج–تگد‚ھ“¯‚¶‚إ‚ ‚邱‚ئ‚©‚çپA پ@پ@پ@پ@پ@پ@پ@-1714.741پپ-78.582x پ@‚و‚ء‚ؤپAxپپ21.821 پ@‚و‚ء‚ؤپAچإ‚à‹ك‚¢’l‚ح2.‚ئ‚ب‚éپB |
| ‰ً“ڑپFپ@‚Q |