| - PR - |
| <R02-No4:法規・条約:解答> 座標変換(回転移動)に関する問題である。問題文にある行列式は、Z軸を回転軸とした場合の回転式である。これをX軸を回転軸とした場合の式に変換し代入して計算すればよい。 次の手順で考えればよい。 ① Z軸を中心軸とした場合の式を考える。 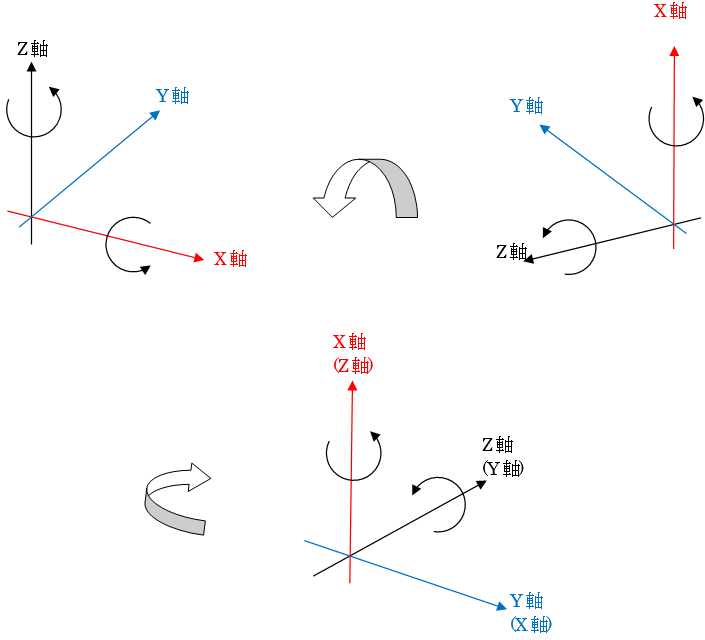 三次元の軸を回転すると上図のようになる。基のX軸が反時計回りに回転させた時の座標点を求める式は問題文に与えられており、変換後のX軸も同様に反時計回りに回転しているため、問題文の式を次のように変換すればよい。なお、( )内は回転前の軸である。  となる。 これを計算すると次のようになる。 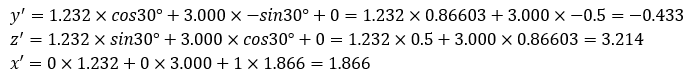 よって、点P’をX軸の周り30°回転させた移動後の点P”の座標は、4.の(1.866,-0.433,3.214)となる。 |
| 解答: 4 |