<R01-No27:応用測量(用地):解答>
① 問題文を図に描くと次のようになる。
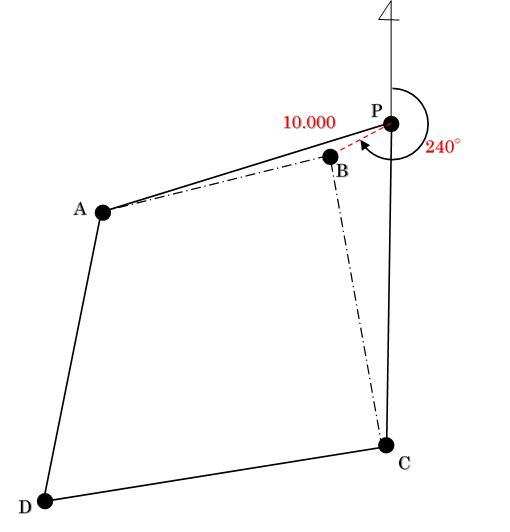
② 点Pの座標値と点Bへの方向角、距離により点Bの座標値を求める。
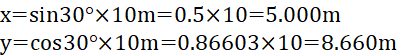
よって、点Bの座標値は次のようになる。

※点Bが点Pに対して、どの象限に位置するかを考えて符号を決定する。
③ 点A〜Dの座標値を用いて面積計算を行う。
|
|
X
|
Y
|
Yn+1−Yn-1
|
X(Yn+1−Yn-1)
|
| A
|
+97.000
|
+46.000
|
64.340-41.000=23.340
|
23.340×97.000=2263.980
|
| B
|
+100.500
|
+64.340
|
72.500-46.00=26.500
|
26.500×100.5=2663.250
|
| C
|
+75.500
|
+72.500
|
41.000-64.340=-23.340
|
-23.340×75.500=-1762.170
|
| D
|
+70.500
|
+41.000
|
46.000-72.500=-26.500
|
-26.500×70.500=-1868.250
|
|
2S
|
1296.810
|
|
S
|
648.405
|
よって、境界点A,B,C,Dで囲まれた四角形の土地の面積は、5.の648.405㎡となる。
点Dを座標原点として、各座標値からx=13,070.500、y=15,041.000を引いた値を用いて点Dから各点の相対座標値を算出し、面積を計算してもよい。
|
解答: 5
|
|