| - PR - |
| - PR - |
| <H30-No5:法規・条約:解答> 点高法による平均高さの計算問題である。点高法とはメッシュに切った交点の高さ(標高)の平均値を求め、これに底面積を掛けて土量計算を行う手法で三角形法と四角形法がある。この問題は土量計算1歩手前の平均高さを求める問題である。 次の考え方で解けばよい。 図のようなh1〜h3までの高さを持つ三角柱を考えると、その平均高さ(h)は次のようになる。 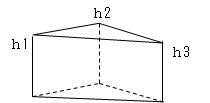 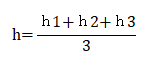 問題文の図を次のように①〜⑥の三角柱と考え、次のように計算すればよい。   また、前式をまとめると次のようになる。 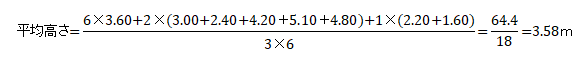 この式は6つの三角柱が共有する高さ、2つの三角柱が共有する高さ、1つの三角柱のみが持つ高さをそれぞれ加え、6個の三角柱の高さを平均するため、6×3=18で割り平均値を求めている。 よって、最も近い値は3となる。 |
| 解答: 3 |